上一章通过动态分析导出了用来得出状态空间平均法的目的![]() 的公式。本章将从另外的角度来看上一章导出的公式的导出方法。前提是至少已经理解了之前导出公式的原理原则。 由于需要上一章的公式创建过程和各个公式,因此本章将使用同样的公式。
的公式。本章将从另外的角度来看上一章导出的公式的导出方法。前提是至少已经理解了之前导出公式的原理原则。 由于需要上一章的公式创建过程和各个公式,因此本章将使用同样的公式。
下面是上一章提到的动态分析。之前导出的线圈电流和电容器的电荷量相关的公式如下。请再来看一遍。 
与上一章相同,这里也给出了最后的公式,就像之前提到的一样,只要将这些公式相结合,即可求出 ![]()
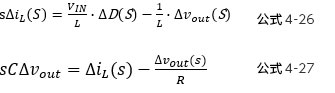
接下来将是本章的内容。以下的公式4-28、4-29是将阻抗S表述为 ![]() 的公式。
的公式。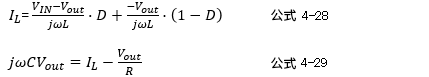
这里 ![]() ,整理如下。
,整理如下。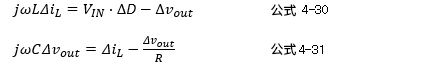
这些公式得出的结果与上一章导出的公式4-26、4-27相同。
思路如下:
① 考虑系统的稳定状态
  1) 线圈电流在1周期内不变
  2) 电容器的电荷量在1周期内不变
  ※此时,阻抗表述为 ![]()
②![]() ,求
,求![]()
只要按这样的思路理解了原理原则,即可比较简单地求出![]() 。
。
关于状态空间平均法的介绍到此接近尾声,状态空间平均法属于近似法,因此请不要忘记一定要考虑应用范围和适用条件,这是非常重要的。
关键要点:
・利用状态空间平均法导出的公式得出动态Δvout/ΔD、ΔiL/ΔD。
・如果理解了公式导出的原理原则,从其他角度也可同样得出Δvout/ΔD、ΔiL/ΔD。
共1条
1/1 1 跳转至页
(传递函数) 状态空间平均法-换个角度看
关键词: 传递 函数 状态 空间 平均法
共1条
1/1 1 跳转至页
回复
| 有奖活动 | |
|---|---|
| 这个春节你犒赏自己什么了?分享你的故事,有奖征集 | |
| 2026年“我要开发板活动”第三季,开始了! | |
| 硬核工程师专属补给计划——填盲盒 | |
| “我踩过的那些坑”主题活动——第002期 | |
| 【EEPW电子工程师创研计划】技术变现通道已开启~ | |
| 发原创文章 【每月瓜分千元赏金 凭实力攒钱买好礼~】 | |
| 【EEPW在线】E起听工程师的声音! | |
| 高校联络员开始招募啦!有惊喜!! | |
 我要赚赏金打赏帖 我要赚赏金打赏帖 |
|
|---|---|
| 【S32K3XX】Standby RAM的初始化流程被打赏¥18元 | |
| Gravity:中英文语音合成模块V2.0及其串口控制被打赏¥24元 | |
| 全彩色度变化图的绘制被打赏¥27元 | |
| 【FreeRtos】FreeRtos任务栈的生长方向管理方式被打赏¥20元 | |
| 【瑞萨RA8D1 LVGL/LWIP评测】LVGL添加输入设备:EC11旋转编码器被打赏¥39元 | |
| 【瑞萨RA8D1 LVGL/LWIP评测】RA8D1部署FreeRTOS+LVGL被打赏¥33元 | |
| 空气质量检测器设计与实现被打赏¥24元 | |
| 【瑞萨RA8D1 LVGL/LWIP评测】LWIP进行UDP、TCP、HTTP、MQTT功能联合测试被打赏¥41元 | |
| 【瑞萨RA8D1 LVGL/LWIP评测】RA8D1部署FreeRTOS+LWIP被打赏¥36元 | |
| RTOS怎么选?让我来给你答案!被打赏¥15元 | |



