电阻器自发热的计算是一个非常基本的概念,但很多工程师对它并不熟悉,或经常被他们忽略。
在我阐述最近设计的高精度电阻式温度检测器 (RTD) 采集系统的原理时,我意识到了它的重要性。对于图 1 中的简化设计,需要考虑信号路径中电阻器自发热引起的误差,才能防止它们所导致的不希望出现的误差级。
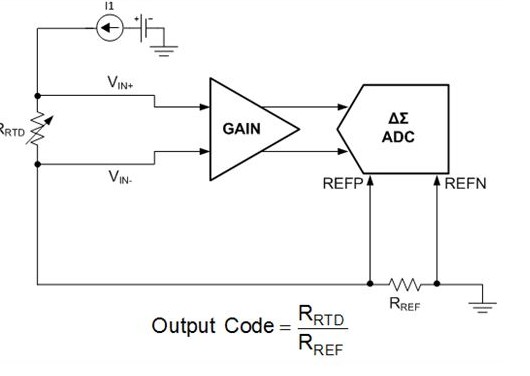
图 1:简化的比率计 RTD 系统
该设计针对比率计测量设计,因此模数转换器 (ADC) 的最终转换结果直接取决于参考电阻器 RREF的绝对值。由于 RREF上有激励电流经过,因此它会消耗电源并发热,从而可引起电阻变化,影响系统精确度。此外,电阻器自发热影响在电流感应或功率测量等众多其它应用中也很重要,其取决于电阻器绝对值,因为在电阻器消耗电源时它可能会改变阻值。
电阻器的温度系数(或 TC)规定了电阻器温度变化时电阻的变化范围。电阻器 TC 的单位一般是每摄氏度百万分之一(ppm/°C)。一个 1% 电阻器具有大约 +/-100ppm/°C 的 TC,而高精度金属箔电阻器则提供不足 0.1ppm/°C 的 TC。
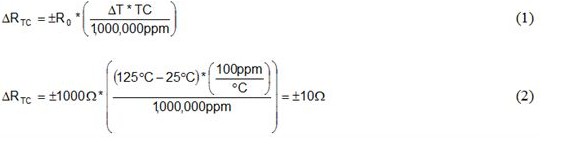
公式 1 和 公式 2 是温度从 25°C 到 125°C 变化时,如何使用电阻器 TC 规范计算 1kΩ、±100ppm/°C 电阻器阻值 ΔRTC 变化的实例。
一般来说,较小表面安装组件(0201、0402、0603 等)在功率耗散方面效率较低,因此具有极高的自发热系数 θSH,有时高达 1000°C/W 以上!这些较小电阻器的额定功率级通常小于 0.1W,但其温度会随功率耗散极其快速地变化。

公式 3 可计算功率耗散所引起的电阻器温度增加量 ΔTSH。公式 4 将 ΔTSH 插入公式 1 替代 ΔT,以确定 100°C/W 适度自发热和 0.5W 功率耗散情况下自发热所引起的电阻变化。
尽管电阻器产品说明书中通常不提供自发热系数,但通常都包含功率额定值下降曲线,您可通过该曲线反向计算出自发热系数。
功率额定值下降曲线可在不超过最大指定温度情况下,针对环境温度规定电阻器的最大功耗。图 2 是 0.5W 电阻器的电阻器功率额定值下降曲线实例。
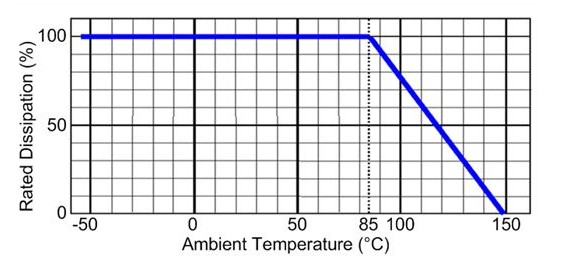
图 2:0.5W 电阻器的功率额定值下降曲线
您可以从图 2 的曲线中轻松确定最大工作温度 TMAX,也就是在额定耗散等于 0% 时 x 轴上的值。在所示实例中,最大工作温度是 150°C。
另外,电阻器也不可能在 100% 额定耗散 (TMAX_PWR100%)、85°C 下工作。您可通过该温度、最大工作温度以及电阻器的功率额定值计算出针对 θSH 的值,公式如下。
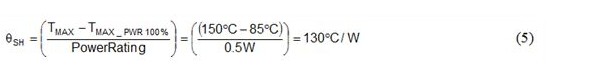
您现在可凭借计算得出的自发热系数确定热增加量,从而可使用公式 3 和公式 4 计算功率耗散所引起的电阻变化。因此,您可根据电阻变化确定对最终系统精度的影响。
因此下次再设计需要高精度电阻器值的系统时,一定要考虑电阻器自发热因素!



 我要赚赏金
我要赚赏金

