EEPW论坛

项目实战—行人检测之SVM理论

现在我们将使用HOG+SVM来进行行人检测，之前我们已经简述过HOG，现在我们来简述SVM，又称为支持向量机。

由于其属于机器学习的内容，故我们只是简述，详细的推导并不涉及。

SVM（支持向量机）主要用于分类问题，主要的应用场景有字符识别、面部识别、行人检测、文本分类等领域。

通常SVM用于二元分类问题，对于多元分类通常将其分解为多个二元分类问题，再进行分类。下面我们首先讨论一下二元分类问题。

对于二元分类问题，如果存在一个分隔超平面能够将不同类别的数据完美的分隔开（即两类数据正好完全落在超平面的两侧），则称其为线性可分。反之，如果不存在这样的超平面，则称其为线性不可分。

所谓超平面，是指能够将n维空间划分为两部分的分隔面，其形如 。简单来说，对于二维空间（指数据集有两个特征），对应的超平面就是一条直线；对于三维空间（指数据集拥有三个特征），对应的超平面就是一个平面。可以依次类推到n维空间。

在下面的图片中，左边的图表示二维空间的一个线性可分数据集，右图表示的是二维空间的一个线性不可分数据集。可以直观的看到，对于左图，我们很容易找到这样一条直线将红色点和蓝色点完全分隔开。但是对于右图，我们无法找到这样的直线。

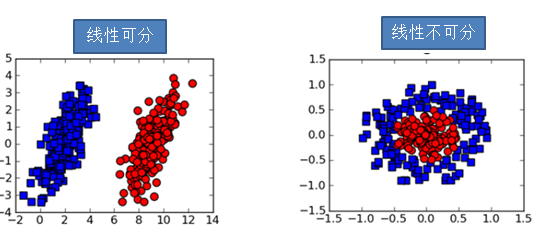
线性不可分出现的原因：

（1）数据集本身就是线性不可分隔的。上图中右图就是数据集本身线性不可分的情况。这一点没有什么疑问，主要是第二点。

（2）由于数据集中存在噪声，或者人工对数据赋予分类标签出错等情况的原因导致数据集线性不可分。下图展示的就是由于噪声或者分错出错导致线性不可分的情况。

现在，只关注图中的实心点、空心点，以及绿色线段。可以看到实心点和空心点大致分布在绿色线段的两侧，但是在实心点的一侧混杂了两个空心点，在空心点的一侧混杂了一个实心点，即此时绿色直线并没有完全将数据分为两类，即该数据集是线性不可分的。在后面我们会提到通过修正线性可分模型以使得模型能够“包容”数据集中的噪点，以使得SVM能够处理这种类型的线性不可分情况。

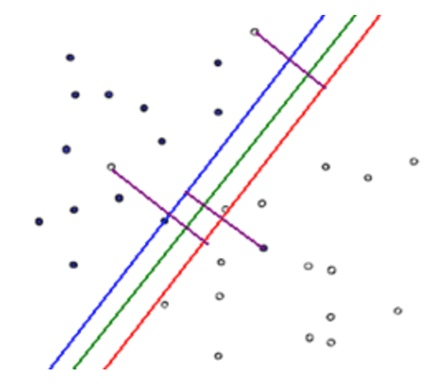
SVM的目标就是找到这样的一个超平面（对于上图来说，就是找到一条直线），使得不同类别的数据能够落在超平面的两侧。

对于线性可分数据集，有时我们可以找到无数多条直线进行分隔，那么如何判断哪一个超平面是最佳的呢?

我们先来看一个简单的例子。图中‘x’和‘o’分别代表数据的两种不同类型。可以看到存在图中这样一条直线将数据划分成两类。对于图中的A、B、C三点，虽然它们都被划分在了‘x’类，但是我们A、B、C真正属于‘x’类的把握却是不一样的，直觉上我们认为有足够大的把握A点确实属于'x'类，但是对于C点我们却没有足够的把握，因为图中分隔直线的稍稍偏离，C点有可能就被划分到了直线的另一侧。

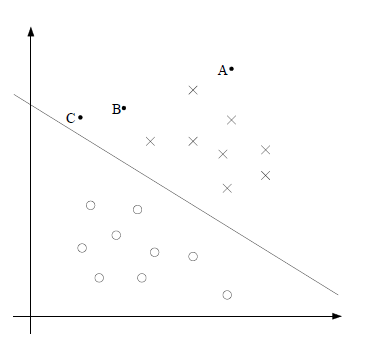
所以，SVM的目标是使得训练集中的所有数据点都距离分隔平面足够远，更确切地说是，使距离分隔平面最近的点的距离最大。

那么到这里我们就不再过多讲述了，SVM本质上较为复杂，我们目前只需要知道其产生的背景以及应用的条件，至于一些其他的概念，例如最优间隔、拉格朗日对偶、以及核函数等等我们不再赘述，防止大家产生厌学心理。

对计算机视觉感兴趣？这个社区推荐给你~

>>点击了解OpenVINO生态开发社区