EEPW论坛

在第一部分中，我们介绍了相控阵概念、波束转向和阵列增益。在第二部分中，我们讨论了栅瓣和波束斜视概念。在这第三部分中，我们首先讨论天线旁瓣，以及锥削对整个阵列的影响。锥削就是操控单个元件的振幅对整体天线响应的影响。

在第一部分中未应用锥削，且从图中可以看出第一旁瓣为–13dBc。锥削提供了一种减少天线旁瓣的方法，但会降低天线增益和主瓣波束宽度。在简要介绍锥削之后，我们会详细说明与天线增益相关的几个要点。

傅里叶变换：矩形函数↔sinc函数

在电气工程中，有各种不同的方法可以将一个域中的矩形函数转变为另一个域中的sinc函数。最常见的形式是时域中的矩形脉冲转换成sinc函数的频谱分量。这个转换过程是可逆的，在宽带应用中，宽带波形也可以转换为时域中的窄脉冲。相控阵天线也具有类似的特性：沿阵列平面轴的矩形加权按照正弦函数辐射方向图。

应用到此特性，以sinc函数表示的第一旁瓣只有-13dBc是有问题的。图1显示了这个原理。

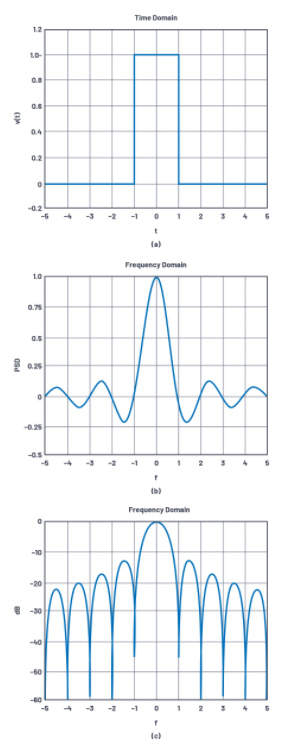
图1.时域中的矩形脉冲在频域中产生正弦函数，第一旁瓣仅为–13dBc。

锥削（或加权）

要解决旁瓣问题，可以在整个矩形脉冲内使用加权处理。这在FFT中很常见，相控阵中的锥削选项则是直接模拟了FFT中加权。遗憾的是，加权也是存在缺点的，它虽然实现了减少旁瓣但需要以加宽主瓣为代价。图2显示了一些加权函数示例。

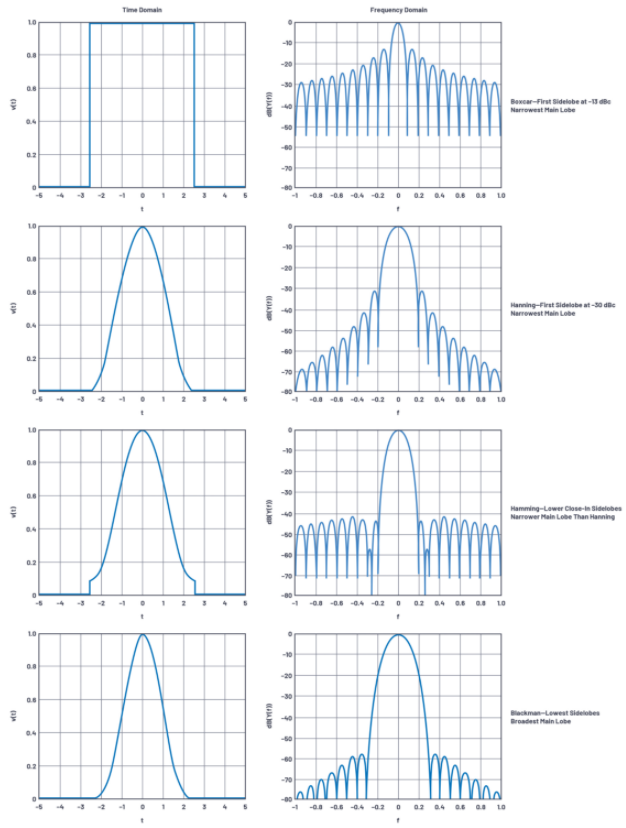
图2.加权函数示例。

波形与天线类比

从时间到频率的转换是很平常的，大多数电气工程师自然会明白。但是，对于刚接触相控阵的工程师来说，如何使用天线方向图类比在一开始并不明确。为此，我们用场域激励代替时域信号，并用空间域代替频域输出。

时域→场域

·v（t）—电压是时间的函数

·E（x）—场强与孔径中的位置呈函数关系

频域→空间域

·Y（f）—功率谱密度是频率的函数

·G（q）—天线增益是角度的函数

图3显示了这些原理。在这里，我们比较了阵列中应用两种不同加权的辐射能量。图3a和图3c显示场域。每个点表示这个N=16阵列中一个元件的振幅。在天线之外，没有辐射能量，辐射从天线边缘开始。在图3a中，场强出现突变，而在图3c中，场强随着距离天线边缘的距离增大而逐渐增大。对辐射能量造成的影响分别如图3b和图3d所示。

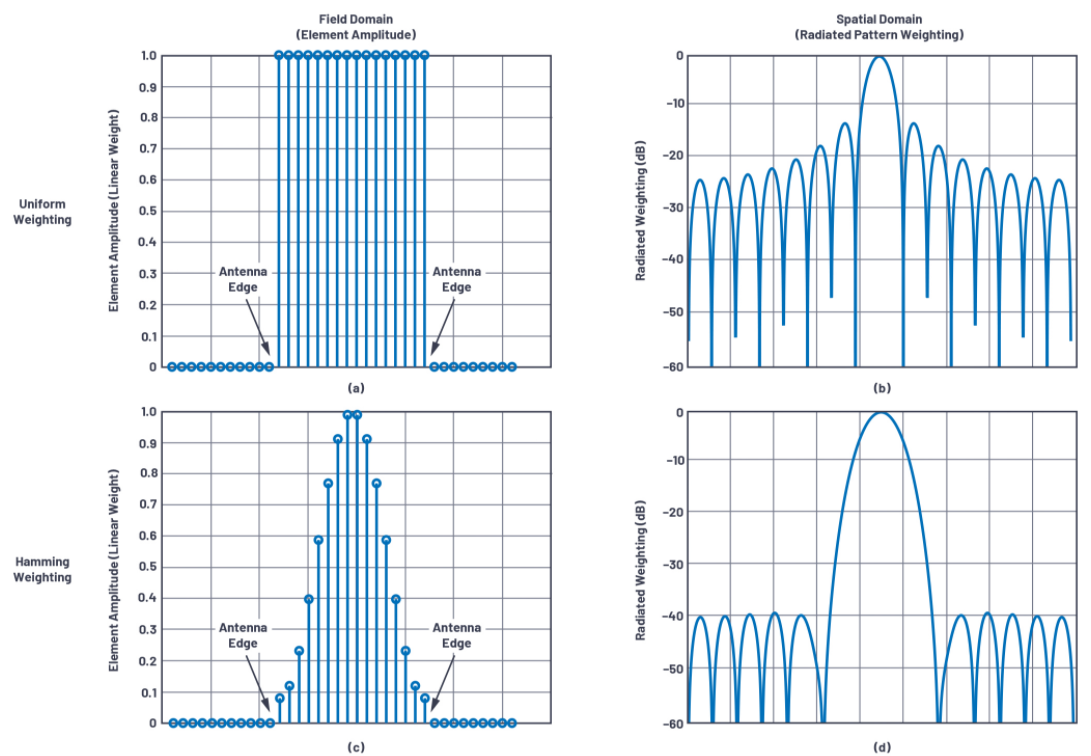
图3.显示变窄元件转化为辐射能量加权的图表；

（A）对所有元件使用统一加权；（b）正弦函数在空间内辐射；（c）对所有元件使用海明窗加权处理；以及（d）以加宽主波束为代价，将辐射旁瓣降低到40dBc。

在下一节中，我们将介绍影响天线方向图性能的两种附加误差项。第一种是互耦。在本文中，我们只是提出存在此问题，并且给出用于量化此影响的EM模型的数量。第二种是由于在相移控制中精度有限而产生的量化旁瓣。我们对量化误差进行了更深入地处理，并对量化旁瓣进行了量化。

互耦误差

这里讨论的所有方程和阵列因子图都假设元件是相同的，并且每个元件都具有相同的辐射方向图。但事实并非如此。其中一个原因是互耦，即相邻元件之间耦合。元件分散在阵列中与元件彼此紧密排列相比，其辐射性能会发生很大变化。位于阵列边缘的元件和位于阵列中心的元件所处的环境不同。此外，当波束转向时，元件之间的互耦也会改变。所有这些影响会产生一个附加的误差项，需要天线设计人员加以考虑，在实际设计中，需要花大量精力使用电磁仿真器来表征这些条件下的辐射影响。

波束角度分辨率和量化旁瓣

相控阵天线还有另一个缺陷，用于波束转向的时间延迟单元或移相器的分辨率是有限的。这通常利用离散时间（或相位）步长来实现数字控制。但是，如何确定延迟单元或移向器的分辨率或位数，以达到的所需的波束质量呢？

与常见的理解相反，波束角度分辨率并不等于移相器的分辨率。从方程式1（第二部分中的方程式2）中，我们可以看出这样的关系：

我们可以用整个阵列中的相移来表达这种关系，需要将阵列宽度D替换为元件间隔d。然后如果我们将移相器ΦLSB替换为？6？2Φ，我们可以粗略估算波束角度分辨率。对于N个元件以半个波长间隔排列的线性阵列来说，波束角度分辨率如方程式2所示。

这是背离瞄准线的波束角度分辨率，描述了当阵列的一半相移为零，另一半的相移为移相器的LSB时的波束角度。如果不到一半的阵列通过编程达到相位LSB，则角度可能更小。图4显示使用2位移相器的30元件阵列的波束角度（相位LSB逐渐增加）。注意，波束角度增加，直到一半元件移相LSB，然后在所有元件移相LSB时归零。当波束角度通过阵列中的相位差而变化时，这是有意义的。注意，正如前面计算的那样，此特性的峰值为θRES。

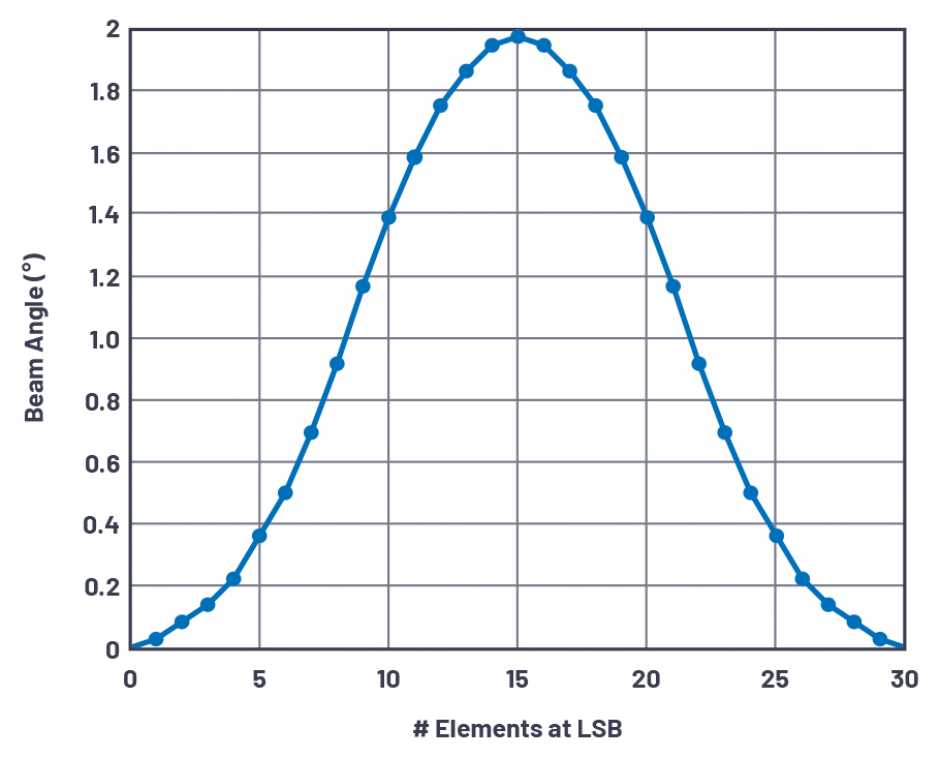
图4.30元件线性阵列在LSB时的波束角度与元件数量之间的关系。

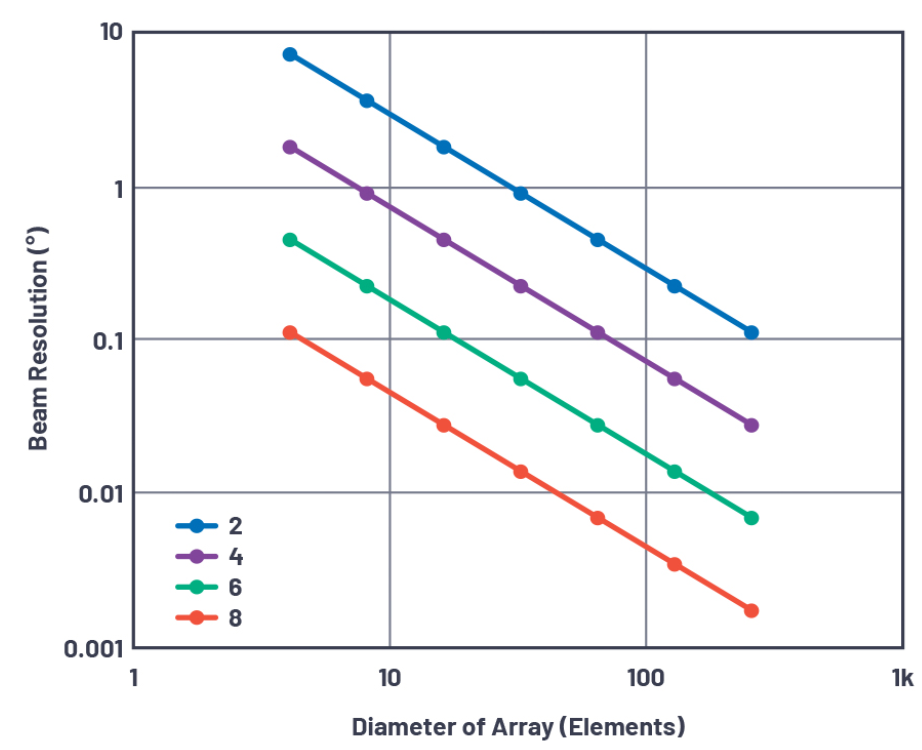
图5.移相器分辨率为2位至8位时，波束角度分辨率与阵列大小的关系。

图5显示不同移相器分辨率下θRES与阵列直径（元件间隔为λ/2）的关系。这表明，即使是LSB为90°的非常粗糙的2位移相器，也可以在直径为30个元件的阵列中实现1°的分辨率。在第一部分使用方程式10针对30元件、λ/2间隔条件进行求解时，主瓣波束宽度约为3.3°，表示即便使用这个非常粗糙的移相器，我们也具备足够的分辨率。那么，使用更高分辨率的移相器又会得出什么结果？从时间采样系统（数据转换器）和空间采样系统（相控阵天线）之间的类比可以看出，较高分辨率的数据转换器产生较低的量化本底噪声。更高分辨率的相位/时间偏移器会导致较低的量化旁瓣电平（QSLL）。

图6显示之前描述的编程采用θRES波束分辨率角度的2位30元件线性阵列的移相器设置和相位误差。一半阵列设为零相移，另一半设为90°LSB。注意，误差（理想量化相移与实际量化相移之间的差异）曲线呈锯齿状。

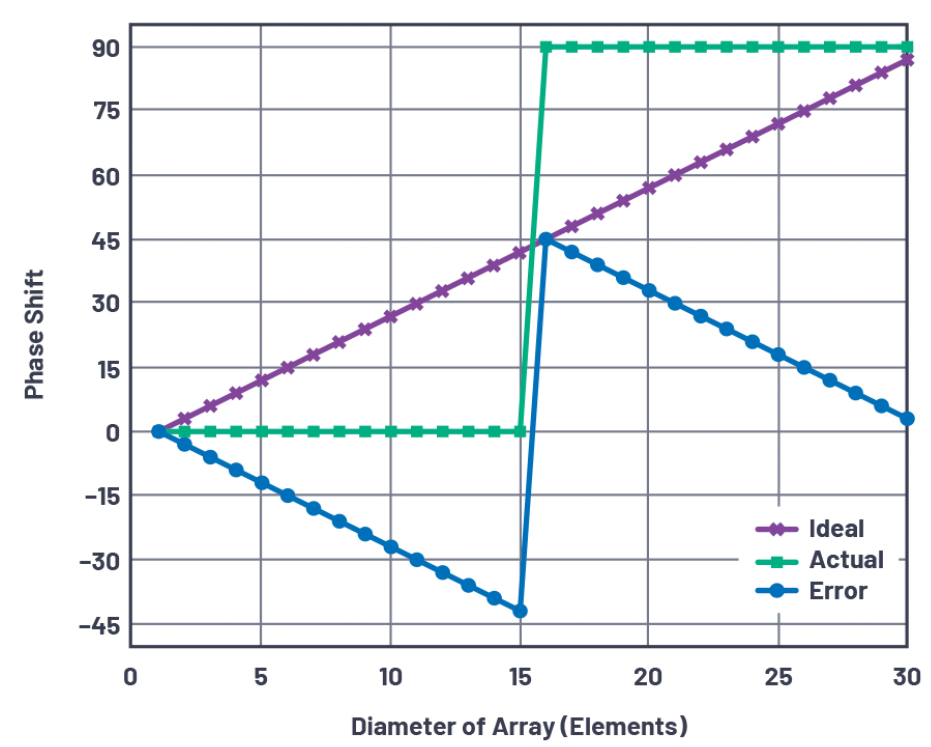
图6.阵列中的元件相移和相位误差。

图7显示同一天线在转向0°和转向波束分辨率角度时的天线方向图。请注意，由于移相器的量化误差，出现了严重的方向图退化。

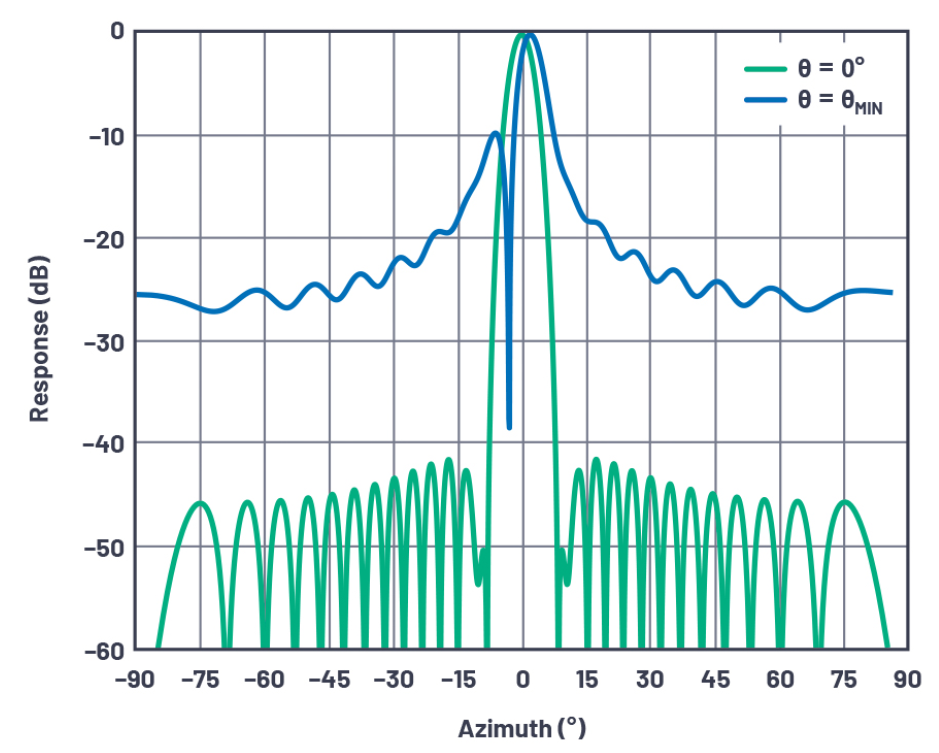
图7.在最小波束角度下具有量化旁瓣的天线方向图。

当孔径内发生最大量化误差，其他所有元件都是零误差，且相邻元件间隔LSB/2时，出现最糟糕的量化旁瓣情形。这代表了最大可能的量化误差和孔径误差的最大周期。图8显示了使用2位30元件时的这种情况。

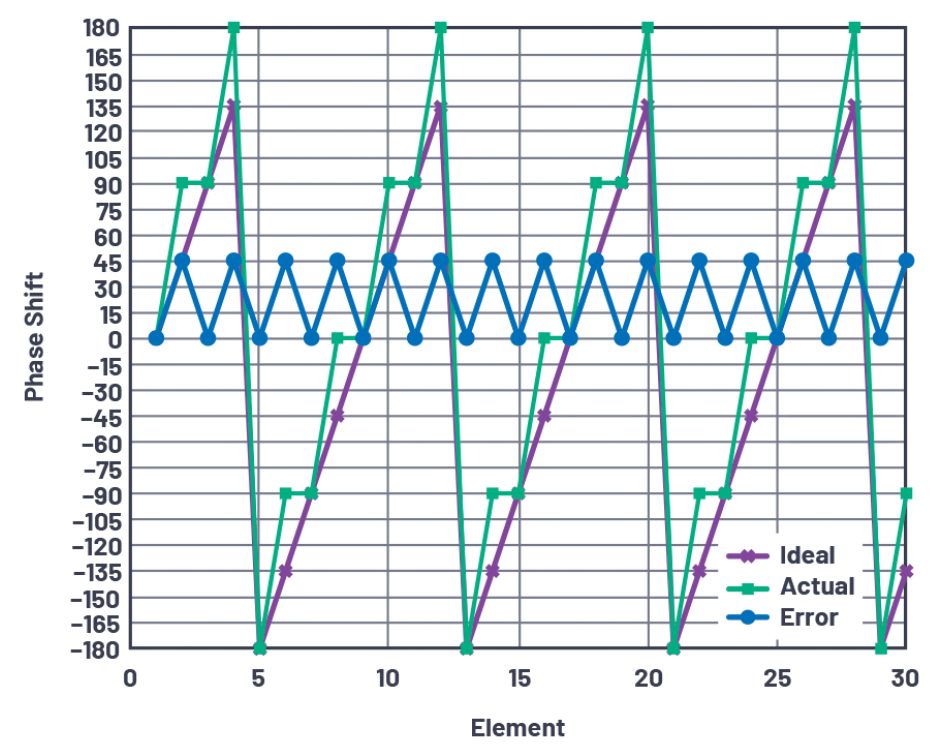
图8.最糟糕的天线量化旁瓣情形——2位。

这种情况在可预测的波束角度下（如方程3所示）发生。

其中n《2BITS，且n为奇数。对于2位系统，这种情况会在±14.5°和±48.6°范围之间发生4次。图9显示该系统在n=1，q=+14.5°时的天线方向图。注意在–50°时具有明显的–7.5dB量化旁瓣。

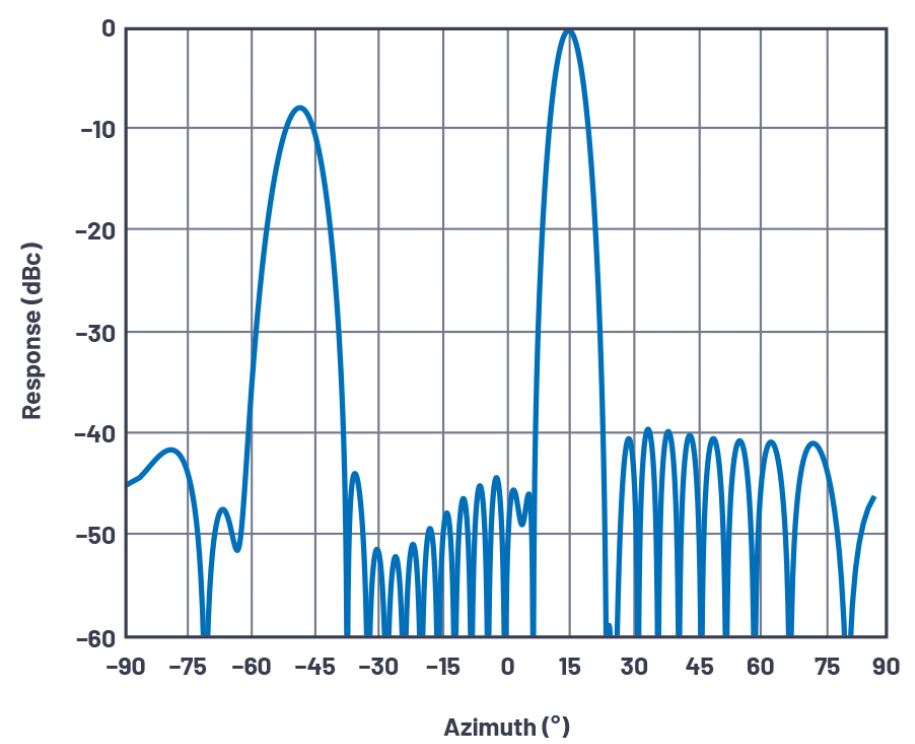
图9.最糟糕的天线量化旁瓣情形：2位，n=1，30元件。

除了量化误差依次为0和LSB/2的特殊情况外，在其他波束角度下，rms误差随着波束在孔径上的扩散而减小。事实上，对于n为偶数值的角度方程（方程式3），量化误差为0。如果我们绘制在不同移相器分辨率下最高量化旁瓣的相对电平，会出现一些有趣的方向图。图9显示100元件线性阵列最糟糕的QSLL，该阵列使用海明锥形，以便将量化旁瓣与本节前面讨论的经典开窗旁瓣区分开来。

注意，在30°时，所有量化误差都趋于0，这可以显示为sin（30°）=0.5时的结果。请注意，对于任何特定的n位移相器，在最糟糕电平下的波束角度在更高分辨率n下会显示零量化误差。在这里可以看出描述的最糟糕旁瓣电平下的波束角度，以及QSLL在每位分辨率下改善了6dB。

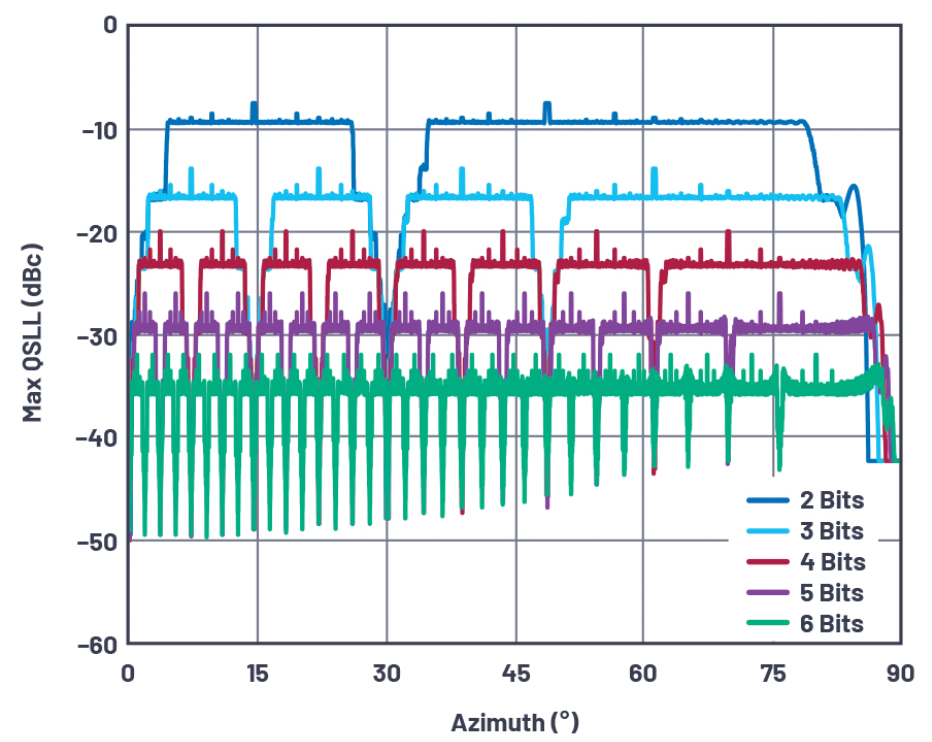
图10.在2位至6位移相器分辨率下，最糟糕的量化旁瓣与波束角度的关系。

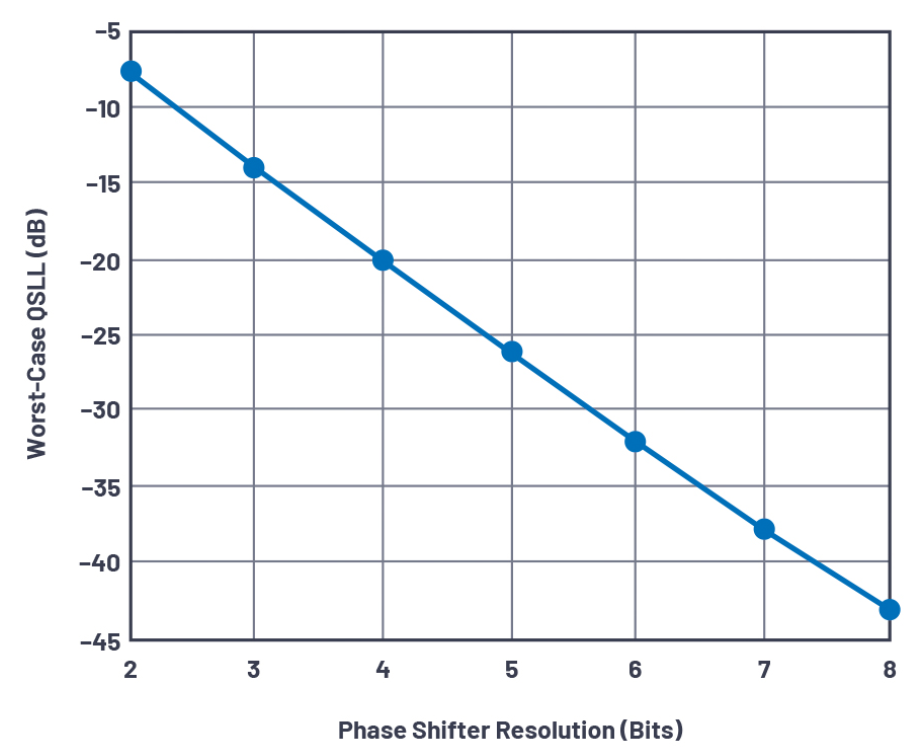
图11.最糟糕的量化旁瓣电平与移相器分辨率的关系。

2位至8位移相器分辨率的最大量化旁瓣电平QSLL如图11所示，它遵循类似的数据转换器量化噪声规律，

或每位分辨率约6dB。在2位时，QSLL电平约为-7.5dB，高于数据转换器进行随机信号采样时经典的+12dB。这种差异可以视为在孔径采样时周期性出现的锯齿误差导致的结果，其中空间谐波会增加相位。注意QSLL与孔径大小不呈函数关系。

总结

我们现在可以总结出天线工程师面临的与波束宽度和旁瓣相关的一些挑战：

·角度分辨率需要窄波束。窄波束需要大孔径，这又需要许多元件。此外，波束在背离瞄准线时会变宽，所以需要额外的元件，以在扫描角度增大时保持波束宽度不变。

·似乎可以通过增大元件间隔来扩大整个天线区域，而无需额外增加元件。此举可以让波束变窄，但是，很遗憾，如果元件分布不均，会导致产生栅瓣。可尝试通过减小扫描角度，同时采用有意随机显示元件方向图的非周期阵列，来利用增加的天线区域，同时最大限度减少栅瓣问题。

·旁瓣是另一个问题，我们已知可以通过将阵列增益朝向边缘逐渐减小来解决。但是，这种锥削以波束变宽为代价，又会需要更多元件。移相器分辨率会导致出现量化旁瓣，在设计天线时也必须加以考虑。对于采用移相器的天线，波束斜视现象会导致角位移与频率相互影响，从而限制高角度分辨率下可用的带宽。

以上就是有关相控阵天线方向图全部三个部分的内容。在第一部分中，我们介绍波束指向、阵列因子和天线增益。在第二部分中，我们讨论栅瓣和波束斜视的缺点。在第三部分中，我们讨论锥削和量化误差。本文不是针对精通电磁和辐射元件设计的天线设计工程师，而是针对在相控阵领域工作的大量相邻学科的工程师，这些直观的解释，将有助于他们理解影响整个天线方向图的性能的各种因素。