EEPW论坛

在上一篇文章中，介绍了线性稳压器中阶跃响应和RESR之间的关系，并作为注意事项介绍了线性稳压器中阶跃响应特性不仅受RESR值的影响，而且也会随输出电容器CO值的变化而变化。在本文中，为了加深对线性稳压器阶跃响应波形和相关部件常数的理解，针对上一篇文章中的测量条件，作为参考给出了不同CO值时的阶跃响应波形的测量数据示例。
输出电容器的值与阶跃响应波形

上一篇中的阶跃响应波形是使电路图中的RESR从0Ω到1Ω变化时的示例，输出电容器CO为22µF。下面是上一篇的CO＝22µF时的波形和在CO＝44µF条件下更改RESR时的波形。请注意，从波形③开始各波形的时间轴已经改变。

对比波形数据，首先可以看出，即使RESR相同，如果CO不同，振铃状态也大不相同。另外，CO＝22µF／RESR＝0.1Ω和CO＝44µF／RESR＝50mΩ、以及CO＝22µF／RESR＝0.2Ω和CO＝44µF／RESR＝0.1Ω时，似乎波形差不多。CO加倍则RESR减半，也就是如果CO和RESR的乘积相同，那么我们可以认为阶跃响应特性差不多，然而当RESR＝0.2Ω后，其波形差别就不大了。

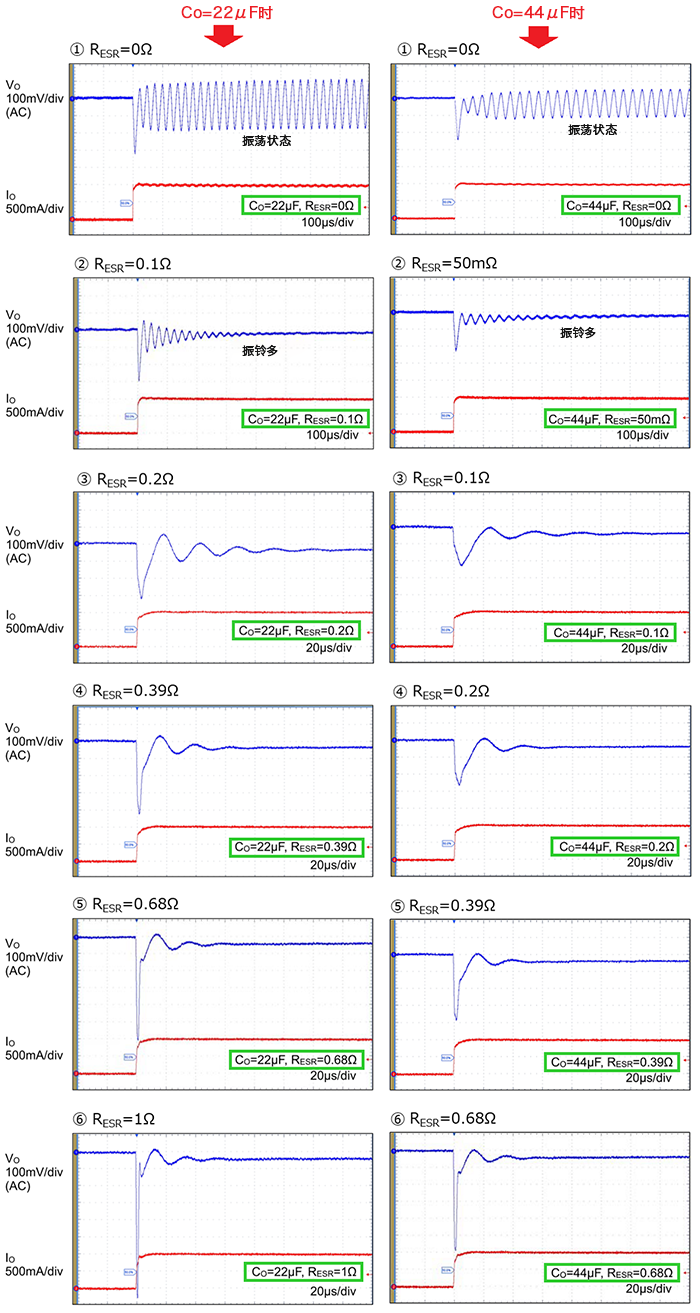
从这些波形中，可以看出上一篇中作为注意事项提到的，阶跃响应特性不仅随RESR变化，还会随CO值的变化而发生变化。另外，还可以看到变化不是线性的。此外，如上一篇中所述，还有其他一些影响因素，比如负载电流值、电流阶跃的压摆率、线性稳压器IC的类型等。因此，很难一概而论地确定常数，需要使用在这个电路条件下确定的最佳常数。
另外，MLCC的尺寸也会因电容量的不同而异，作为RESR的低阻值电阻的尺寸也会因阻值的不同而异，两者的价格也都不同。优化阶跃响应特性时，需要考虑到这些因素，并且平衡CO和RESR来优化。
“线性稳压器的稳定性优化简易方法”到此结束。

・可以说线性稳压器的阶跃响应特性是基于多种因素的综合特性，因此在进行优化时不是只确认一个部件的常数，还要确认其他部件的参数。
・线性稳压器输出电容器CO的电容量也会影响阶跃响应特性。
・际上通过平衡线性稳压器的RESR和CO来进行优化。