EEPW论坛

本文是继上一篇文章“升降压转换器的传递函数导出示例　其1”之后的“其2”。升降压转换器具有多种控制方式。在这里抽取了其中两种，本文将使用第二种控制方法。

此次也同样，推导出的传递函数为和，同样按两个步骤来导出传递函数。

升降压转换器的传递函数导出示例　其2：ton≠ton’ 的升降压转换器

此次的控制方式不是降压开关与升压开关同时导通，而是分别独立工作并控制的方式。因此，降压开关和升压开关的动作因输入电压与输出电压的关系而发生变化，故存在几种模式的传递函数。此次来推导降压开关和升压开关同时开关部分的传递函数。

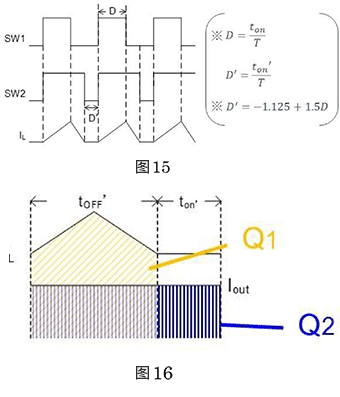
首先来看具体的控制系统（图13）。

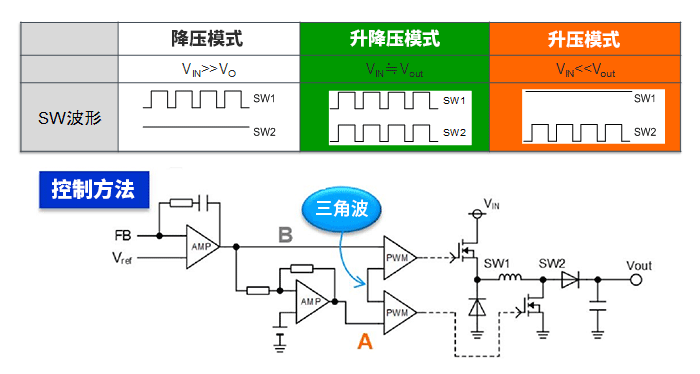
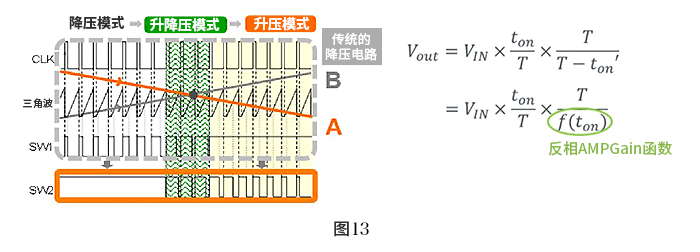
图中给出了根据输入与输出的关系以降压、升降压、升压三种模式工作，SW1和SW2的开关波形。各模式下的开关工作可以一目了然。

ton≠ton’的升降压转换器

右侧电路图是上述电路的简化版。计算公式和以往的作法相同分两步进行。

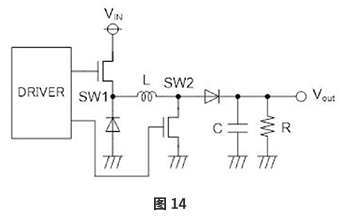
●第1步：考虑系统的稳定状态

① 线圈电流在1周期内不变
② 电容器的电荷量在1周期内不变

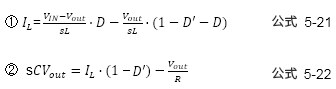
●第2步：
 求出对干扰的变化量，描述传递函数

基于前面的公式5-21、5-22计算示例如下。

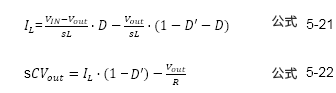
设并代入公式5-21、5-22中，可得到如下公式。

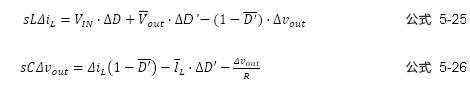
在这里，设

然后，将公式5-25和5-26联立，求与得出如下结果。

从结果可以看出，虽然表示Duty的部分不同，但特性结果还是相同的。

至此推导出了降压、升压、升降压转换器的传递函数，全都都采用统一的方法。请务必自行实际计算一下。下次开始将对包括其他因素在内的传递函数进行探讨。

・各转换器导出的是：Δvout/ΔD、ΔiL/ΔD。

・传递函数通过考虑系统的稳定状态，求出对干扰的变化量这2个步骤推导出来。

・升降压转换器的传递函数基本上也按照与升压转换器和降压转换器同样的步骤进行推导。