EEPW论坛

电子电路设计中，常用的滤波器主要分为高通滤波器、低通滤波器、带阻滤波器、

带通滤波器，而这四种滤波器又统称为有源滤波器。下面单独谈一下这个高通滤波器的工作原理与运用。

高通滤波器的特性：允许通过高频信号，衰减低频信号。如下图所示，当信号处于低频段的时候幅频特性如下：

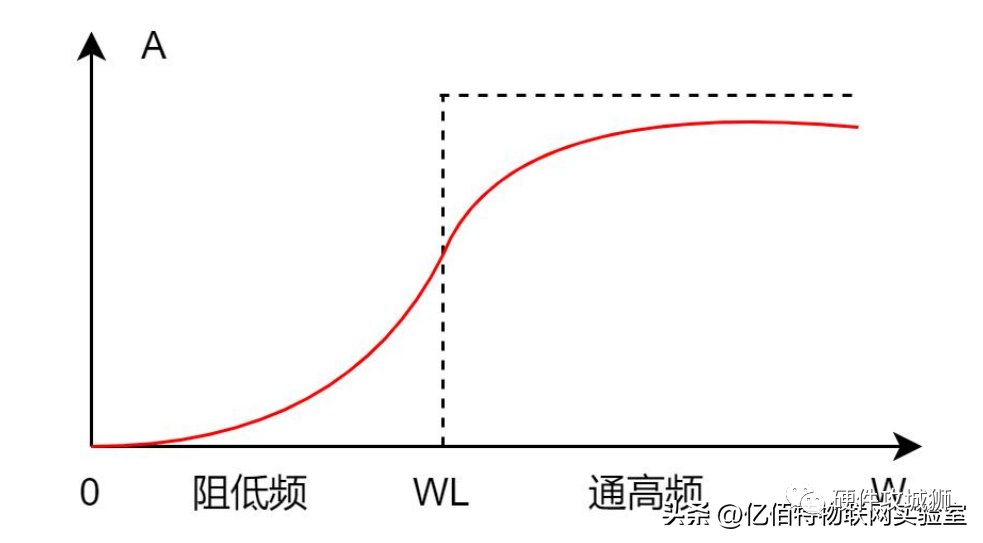
高通滤波器的原理解释完之后，我们再看下面的微分电路：

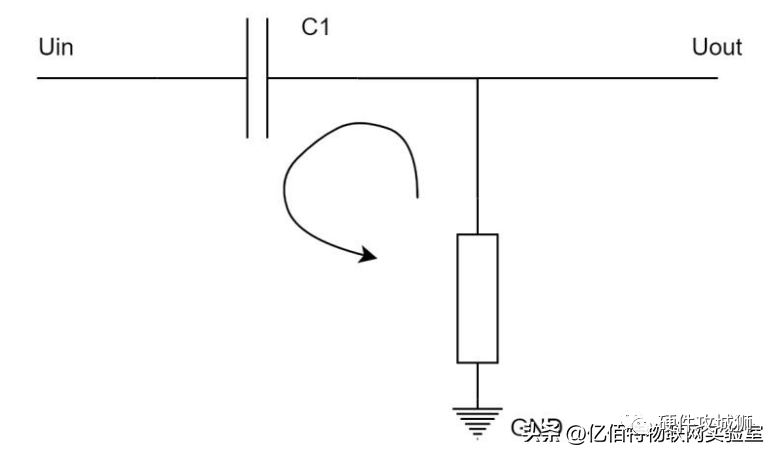
同之前分析低通滤波器一样，如图分析上面的微分电路，学习电路知识的我们知道，于积分电路而言，时间常数 T 是大于输入信号的脉冲宽度的；反之，对于微分电路，时间常数 T是远远小于输入信号宽度的。

从电路分析，当一个输入信号冲出瞬间，由于电容两端电压不能突变，此时就可以把电容看成一个短路，流过的脉冲全部留到了电阻上，电阻的电压也就变得最大，但是对于微分电路来说，因为时间常数远小于输入信号的脉冲宽度，所以很快电容就开始充电，由于电容两端的电压不能马上突变，所以电容还在充电，这时候电容充电满了，充满之后，电容就成了开路状态（同时 Uout 也是 0），也就是断开了输入，这时输入脉冲就会断开消失，而变成开路的结果就是没有电流流过电阻，电阻上面就没有电压，就是相当于输入端接地。

观察电压的输入极性，左边是正右边是负，那么这个时候电阻上的电压还是最大，只不过变成了最大的负电压。这个时候开始放电，放电的同时电容两端的电压不能突变，那么这个时候，电阻上的电压还是最大，然后快速放电（由于时间 T 很小），放完之后，等待下一次的脉冲过来，此时 Uout 还是 0。

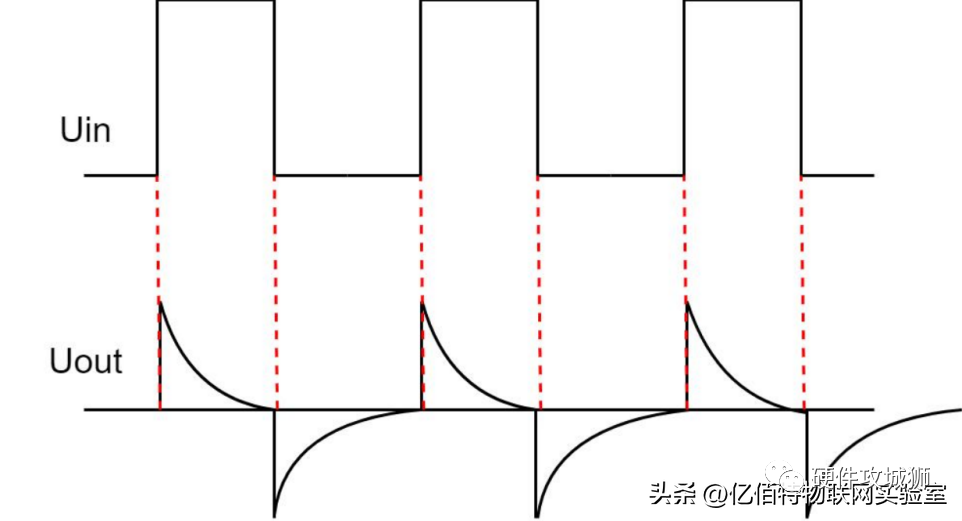
简单总结一下：微分电路其实就是通过电容不能突变的特性，让脉冲不断产生尖波，从而求出输入信号的突变成分，也就是通过改变电容和电阻阻值，来获得某一频率范围下的信号，通过一系列的尖波突变，可以知道 Uin 输入的大小不变，所以结论就是：微分电路无输出。

同样，在弄清楚微分电路之后，再看高频滤波器电路就会一目了然，下面是小编绘制的两个高通滤波器电路：一阶高通滤波器和二阶高通滤波器。

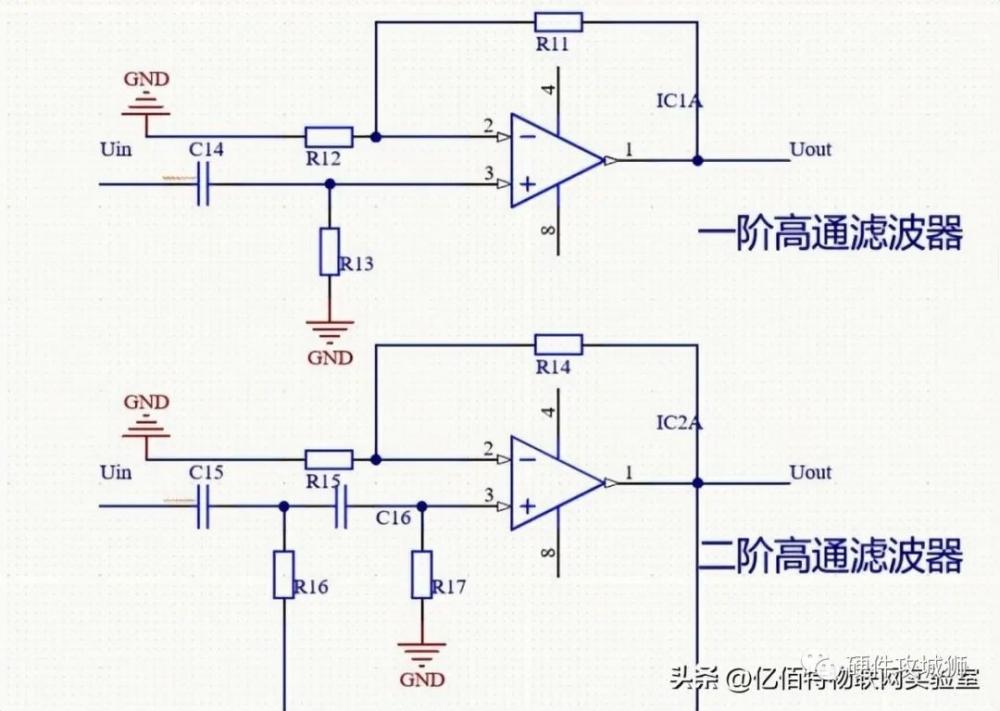
Aup=1+（R11/R12），F0=1/(2πR6C3)，二阶也是对于增加性而增加的正反馈引入。

转载自网络，如有侵权，联系删除。