EEPW论坛

磁路基础
　　这次我们会把磁带到经典电路中，先了解磁路欧姆定律，之后再了解基尔霍夫定律。

　　图1
　　磁动势MMF=磁场强度H*磁路长度L。
　　根据H=B/u. Φ=B*S.
　　我们可得 F=（L/u*S）* Φ。
　　人们喜欢把它转换为以下形式：
　　F=R* Φ
　　这样磁阻R=L/（u*S）。 这就是磁路的欧姆定律。把磁动势F比作电动势；把磁通Φ比作电流；把磁阻比作电阻。
　　这样就有了
　　F=H*L=N*I=R* Φ 。
　　磁路的基尔霍夫第一定律：
　　当磁路为分支磁路，如图2，可以总结为：穿过磁路中不同截面结合处的磁通的代数和等于零。（类似于KCL）

　　图片来自“全屏显示课程章节”
　　图2
　　磁路的基尔霍夫第二定律：
　　当磁路是由不止一种材料组成时，各磁路段的HL（R* Φ）的代数和等于环路交链的磁通势F的代数和。（类似于KVL）
　　ΣF= Σ HL
　　饱和电流：

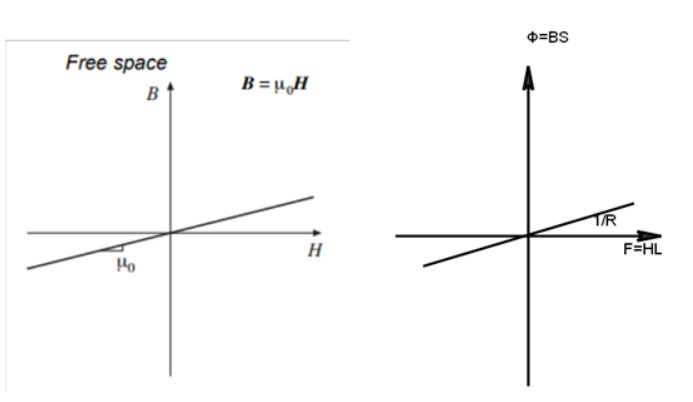
　　图 3
　　既然我们知道了 F=R* Φ，不妨找一下他们之间的联系。
　　由B-H图来看，B正比与磁通量Φ，H正比与磁通势F。所以我们很容易得到图三右图的斜率为R磁阻的倒数。
　　当磁芯饱和后，磁通量Φ（sat）=B（sat）*S.
　　我们已经知道
　　F=H*L=N*I=R*Φ。
　　所以：
　　I（sat）=［B（sat）*S*R］/n
　　下面来一道典例：

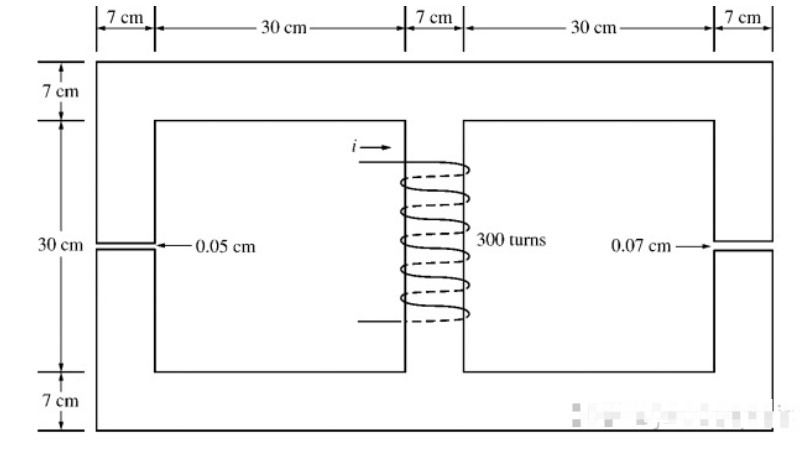
　　已知条件：
　　这个Ecore的磁导率为2000； 厚度为7cm；如果i=1A，求左侧，中间，右侧的磁通量，并求气隙的B（flux density）。根据边缘效应，气隙的作用面试比实际面积大5%.
　　思路：F=H*L=N*I=R* Φ 。
　　R=l/μ0*u*A
　　难点：1）根据NI=RΦ， 算出总磁通；2）每侧的磁通如何分部；3）计算气隙的磁阻时不加相对磁导率。4）磁通与磁感应强度B的关系。
　　解：
　　假设
　　R1： 左侧磁阻
　　R2： 左侧气隙磁阻
　　R3：右侧磁阻
　　R4：右侧气隙磁阻
　　R5：中间磁阻

　　总磁阻：Rtot= 120.8 kA t/Wb
　　Φtot=NI/Rtot=0.00248Wb. （中间的磁通）
　　俩侧的磁通，根据磁路基尔霍夫第一定律：

　　最后计算气隙的B
　　B=Φ/S
　　B左=0.00135/（0.07²*1.05）=0.2623T
　　B右=0.00113/（0.07²*1.05）=0.2196T