EEPW论坛

在电路分析中，谐振（Resonance）是一个重要的概念，它描述了电路在特定频率下对交流信号产生显著响应的现象。谐振时，电路中的某些元件（如电容和电感）之间的相互作用会导致电流或电压的幅值远超过非谐振频率下的情况。

串联谐振

在串联电路中，当电路中的电容和电感的电抗值（容抗和感抗）相等但符号相反时，电路会发生串联谐振。这时，电容和电感的阻抗相互抵消，导致电路的总阻抗达到最小，从而电流达到最大。

串联谐振的特点：

1. 阻抗最小：电容和电感的阻抗相互抵消，使得总阻抗最小。

2. 电流最大：由于阻抗最小，电路中的电流达到最大。

3. 电压分布：在谐振频率下，电容和电感上的电压幅值相等但相位相反，因此它们相互抵消。输入电压完全加在电阻上。

4. 带宽：串联谐振电路具有较窄的带宽，即只对特定频率附近的信号产生显著响应。

并联谐振

与串联谐振不同，并联谐振发生在并联电路中。当电路中的电容和电感的阻抗值相等但符号相反时，电路会发生并联谐振。这时，电路的总导纳（阻抗的倒数）达到最大，导致支路电流最大，而总电流最小。

并联谐振的特点：

1. 导纳最大：电容和电感的导纳相互叠加，使得总导纳最大。

2. 支路电流最大：与串联谐振相反，并联谐振时电容和电感支路的电流达到最大。

3. 电压分布：在谐振频率下，电容和电感支路上的电压幅值相等但相位相反，因此它们相互抵消。输入电压主要加在并联谐振支路上。

4. 带宽：与串联谐振类似，并联谐振电路也具有较窄的带宽。

拓扑比较串联谐振与并联谐振的主要区别：

1. 电流与电压关系：串联谐振时电流最大，电压分布在电阻上；并联谐振时支路电流最大，但总电流最小。

1. 应用场景：串联谐振常用于滤波器和信号选择器；并联谐振常用于调谐电路和振荡器。

2. 带宽：两者都具有较窄的带宽，但具体带宽取决于电路参数和设计。

注意事项

1. 稳定性：谐振电路在某些条件下可能变得不稳定，导致振荡或自激。因此，在设计谐振电路时需要考虑稳定性问题。

2. 频率敏感性：谐振电路对频率非常敏感，微小的频率变化可能导致电路性能显著下降。因此，在实际应用中需要确保电路能够精确调谐到所需频率。

3. 元件参数：电容和电感的参数（如容值和感值）对谐振频率和电路性能有重要影响。因此，在设计和制造谐振电路时需要精确控制这些参数。

串联谐振与阻抗的关系：

在谐振点时，RLC串联电路的等效状态可以描述如下：

1. 阻抗最小：由于电感抗和电容抗在谐振频率下相等但符号相反，它们会相互抵消，导致电路的总阻抗（Z）达到最小值。这个最小值等于电路中的电阻值（R），即Z = R。

2. 电流最大：由于阻抗达到最小值，电路中的电流（I）会达到最大值。这是因为根据欧姆定律（V = I * Z），当电压（V）保持不变而阻抗（Z）减小时，电流（I）会增大。

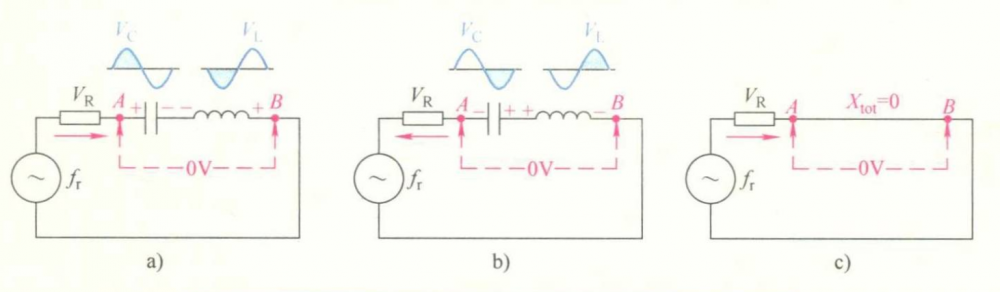
3. 电压分布：在谐振频率下，电感两端的电压（VL）和电容两端的电压（VC）的幅值相等但相位相反。因此，这两个电压会相互抵消，导致输入电压（V）完全加在电阻（R）上。这意味着电阻两端的电压等于输入电压，即VR = V。

4. 功率因数：在谐振状态下，电路的无功功率（Q）为0，因为电感和电容的无功功率相互抵消。这导致电路的功率因数（PF）为1，表示电路在谐振时是完全有效的。

5. 等效电路：在谐振点时，RLC串联电路可以等效为一个纯电阻电路。这是因为电感抗和电容抗的相互抵消使得电路的总阻抗变为实数（即电阻值），从而消除了任何与频率相关的虚部。

RLC 串联谐振在谐振点时的电路等效状态

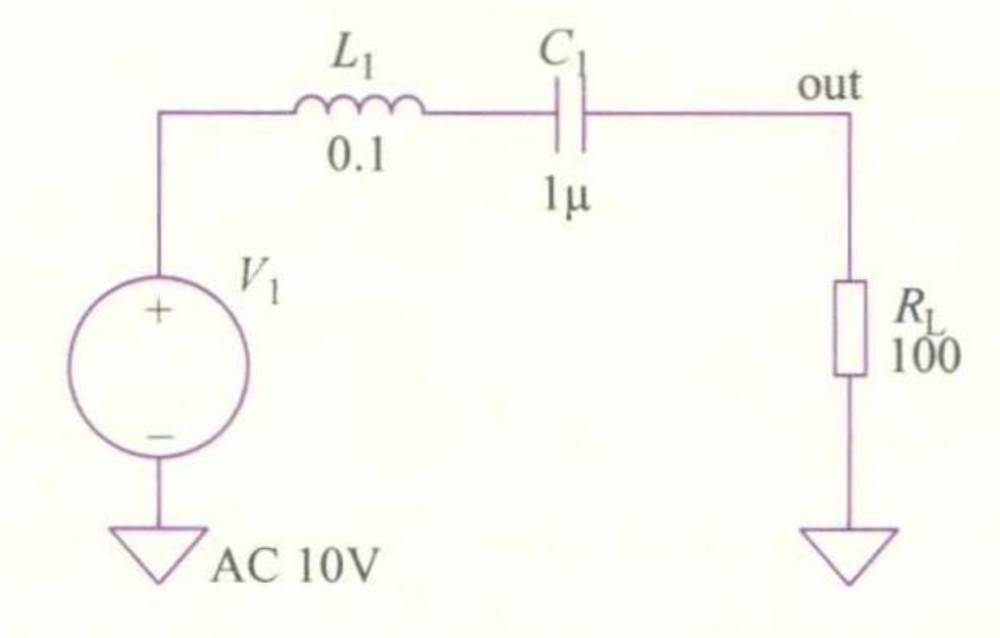
在谐振频域分析时，增益一般用dB表示，而不用倍数表示，这是因为dB表示的范围很宽，如果用倍数表示，数字会显得十分庞大，而对于频率相关的参数，一般用对数Out表示更符合大家的习惯。同时，另一种频率的表达方式，即以归一化频率来描述，归一化频R100率即为工作频率与电路的基本谐振频率的比值，这样也能大大扩展频谱的表达范围。现在VAC 10V通过一个简单的实例仿真来观察图所示的谐振状态，RCL串联谐振仿真电路图如图所示，其仿真结果如图所示。 RCL串联谐振仿真电路图 在这个例子中，我们通过对输人AC信号进行扫频分析，从直流变化到100MHz，看此电路中的电流和电压情况，因为是串联谐振，我们可以比较方便地观察负载Rl上的电流和电压。具体仿真参数如下:L,=0.1H，C=1μF，R=100Ω，交流输人为幅值为 10V 的正弦激励。

仿真电路图:

RCL 串联谐振仿真结果:

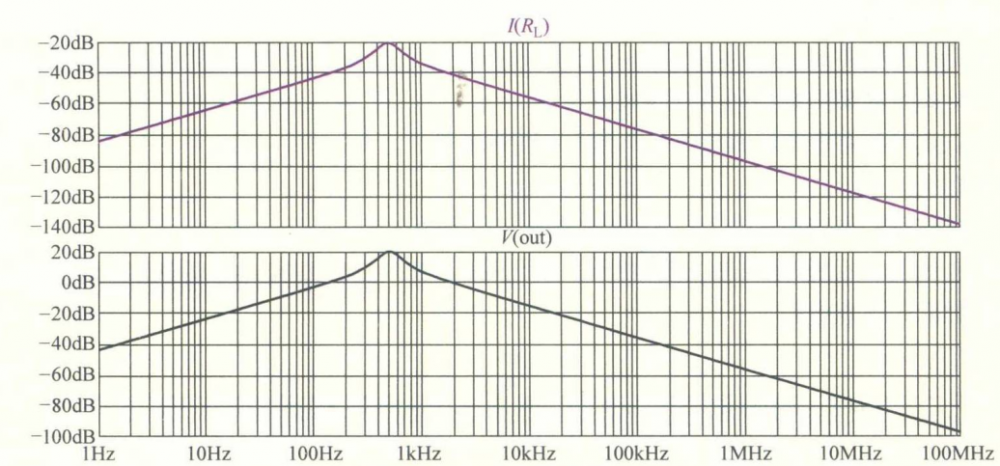
可以看到，整个电路中的电流在全频率范围内有一个峰值，此时对应的负载电压上也出现了最大值，这个频率范围内即为谐振频率，测量到频率约为506Hz，而理论计算约为503.3H，这差异主要是测量不准确造成的。读者其实不好理解在频域下的数据意义，那我们回到时域，即将谐振频率代回到输入激励中，观察此时电路中各节点的电压和电流。时域下的仿真电路和仿真结果如图所示。

时域下的仿真电路:

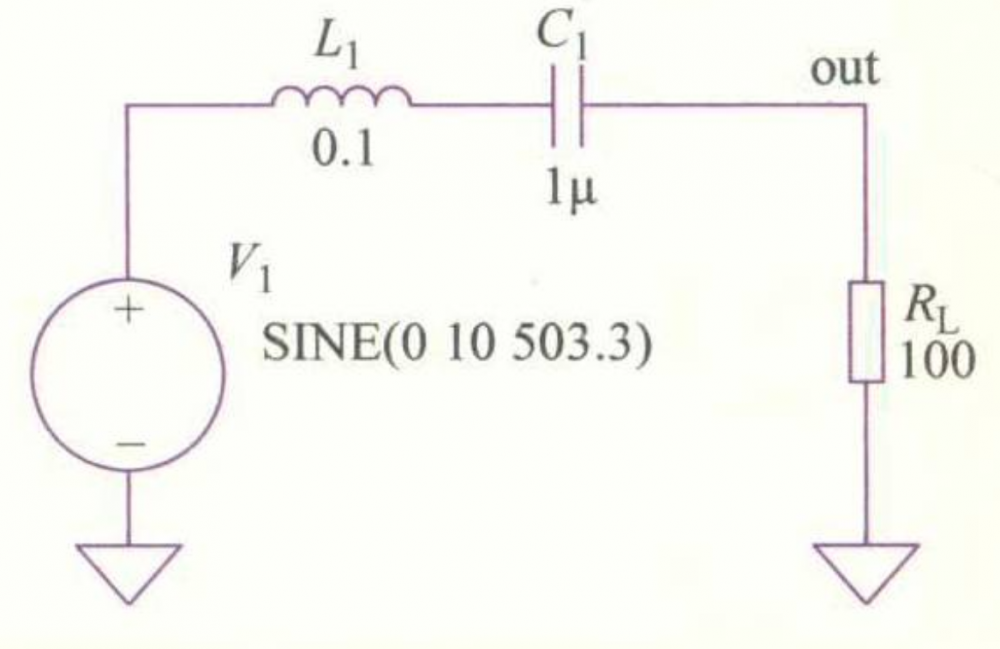
时域下的仿真结果:

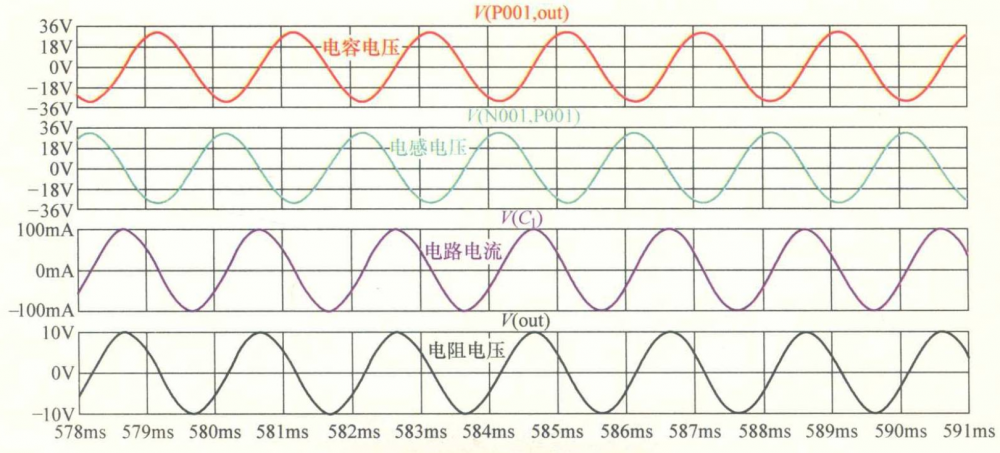
人为地将谐振点频率代人激励信号，可以看到RLC串联谐振时电路形为:

1.电容电压和电感电压幅值相等，相位正好相反，二者叠加为 0。

2.此时输出负载电压等于源电压。

3.此时电路中的电流最大，其值大小为源电压/输出负载。

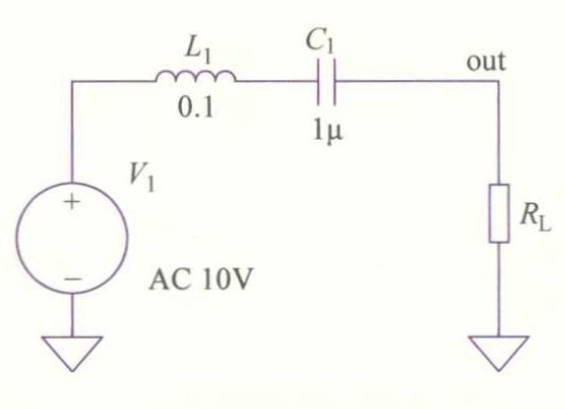
同样我们可以改变负载，观察输出电压和电路中的电流的变化情况如图所示的仿真电路。

负载变化时的电路中的电流及输出电压增益:

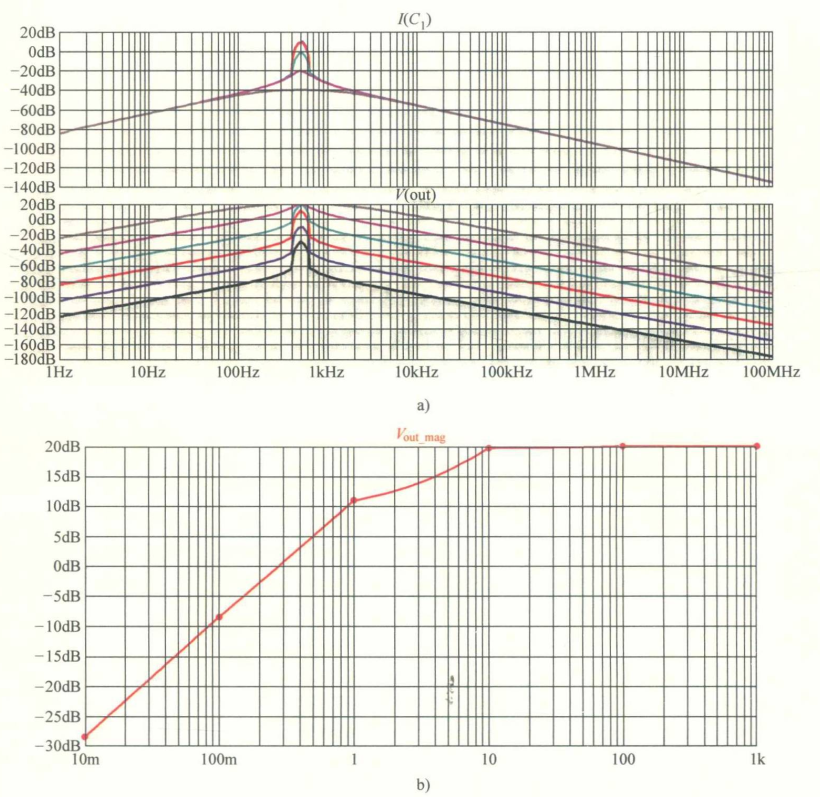
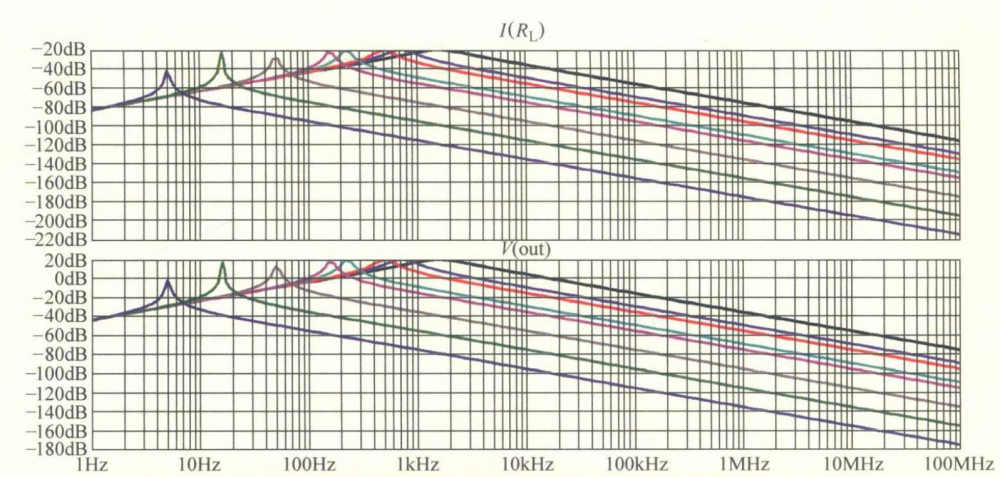
从上面简单的例子中可以看到在一个固定的频率处(见图3-13a)，由于不同负载变化，输出电压的谐振峰值也在变化(见图b)，谐振频率却只由参数 L/C 决定。同时，我们固定负载，可以看到谐振频率发生了改变，谐振元件(电感)变化时的电路仿真原理图如图所示，其变化时电路中的电流和输出电压增益如图所示。

谐振元件(电感)变化时的电路仿真原理图

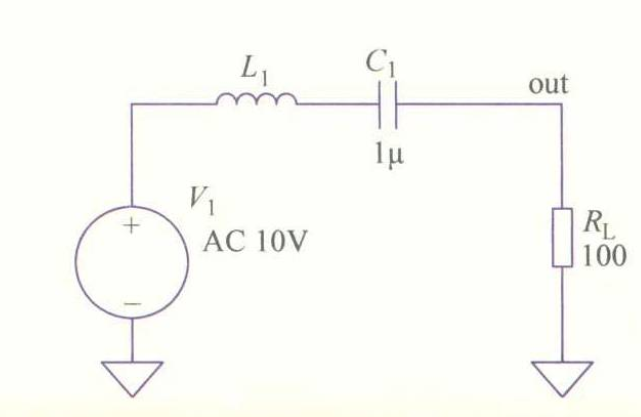
谐振元件(电感)变化时的电路中的电流和输出电压增益: