EEPW论坛

前言
 

通常激光光强分布呈高斯型，而在许多实际应用中，需要将光强分布加以转换，即光束整形，如呈平顶状和环状等。以往人们多用计算全息法实现环形分布，但衍射效率低，难于推广。近年来人们开始研究二元光学元件(BOE)在光束整形方面的作用。二元光学元件是在计算机制全息图和相息图研究发展的基础上，利用计算机设计和微电子加工技术研制成的一种高效率的新型光学元件。由于它能灵活控制波前，因此在光束整形方面有着广泛的应用前景。

   二元光学的优点——高衍射效率；独特的色散性能；更多的设计自由度；宽广的材料选择；独特的光学功能。

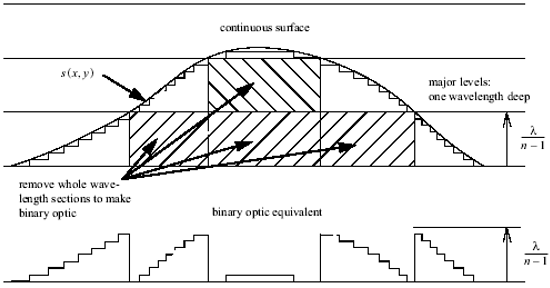
图1表面进行划分从而形成一个二元光学元件

 

二元光学器件分为主阶次和带有几个次阶次的连续界面。在二元光学中，每个主阶次上的次阶次数目通常设置为2、4、8等。GLAD中产生二元光学元件命令如下所示：

binary/lens/surface kbeam xrad yrad level nlevels

int2phase/two kbeam1 kbeam2 [2.*pi*(rindex-1)/lambda]

binary/lens/phasescreen ibeams rindex xrad yrad level nlevels

binary/lens/residual ibeams rindex xrad yrad level nlevels

binary/surface kbeam level nlevels

这些命令执行的是产生二元光学的光栅和透镜，其二元光学表面可以由binary/surface 命令产生，并直接或者间接依靠 int2phase、int2waves、sfocus起着相位屏的作用。二元光学表面可以图示为plot的强度项。

binary/surface 命令能够将任意分布的光场转化为二元光学器件的面形。

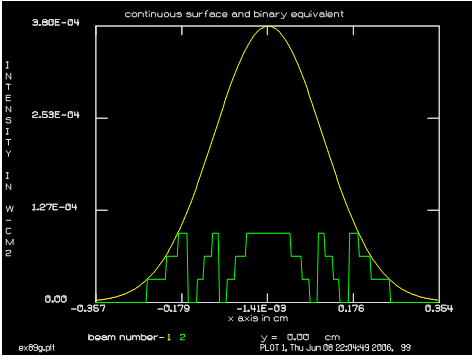
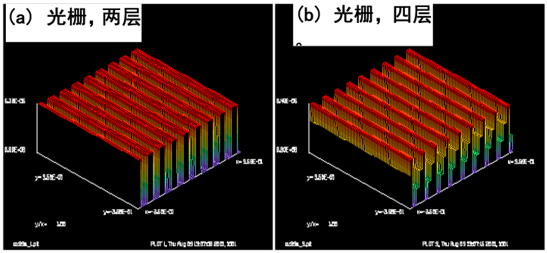
二元光栅表面计算：

这里举一个二元光栅的例子，它是由二元表面组成，然后对其执行“sfocus”命令。表面通过具有一定高度的强度表现出来，高度的单位为厘米，表面的高度可以通过任意一个常规的强度出图命令显示出来。“sfocus”命令将表面的高度作为一个相位差引入，然后乘以α = n – 1，传输距离为z，将其设定为1。“sfocus”命令还包括了2π ⁄ λ这一项。次级数量分别为2,4,8和16，在这样的单位下，16个次级分辨率不好，但是表面却可以以一个近似光滑的分布显示出来。

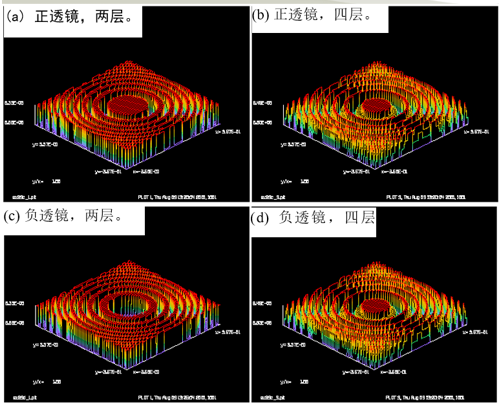
二元透镜计算：

下面（a）（b）图为一个半径为100的正透镜，焦距为200 cm。透镜的净孔径为0.225 cm，设计波长为0.6328 um。远场中的峰值强度显示在子级阶数上，显示出与光栅相似的渐近行为。（c）（d）图说明了一个与上面正透镜相似的负透镜，在虚拟焦距处，远场位于透镜后面100厘米处。

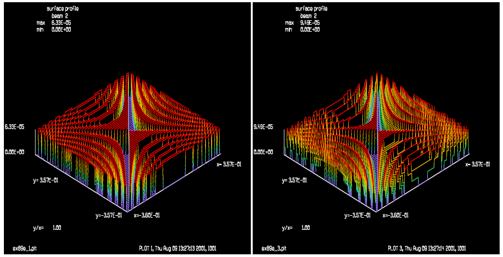
下图展示一个正负组合二元透镜，其等圆柱形焦距为正负200 cm。并可利用可分离传播和转置步骤得到远场分布。