EEPW论坛

在讨论Buck-Boost转换器在非连续导通模式（DCM）下的小信号分析时，我们首先需要理解DCM与连续导通模式（CCM）之间的基本区别。在CCM中，开关器件和输出二极管在一个开关周期内都会导通和关断多次，以保持输出电压的稳定。而在DCM中，开关器件和输出二极管在每个周期内只会导通一次，直到下一个周期开始。

这种工作模式导致了DCM下的小信号模型与CCM有很大的不同。

Buck-Boost功率级DCM下的脉冲宽度调制开关模型推导

在DCM下，Buck-Boost转换器的开关行为可以通过以下步骤进行建模：

定义开关周期和占空比：开关周期T是固定的。

占空比D是开关Q1导通的时间与整个开关周期T的比值。

分析开关动作：当Q1导通时，输入电压Vin通过Q1加到电感L上，电感电流iL开始上升。

当Q1关断时，电感L中的能量通过二极管CR1释放到输出端，电感电流iL开始下降。

建立状态空间方程：在Q1导通和关断的两个阶段，分别建立电感电流iL和输出电压Vout的状态空间方程。

这些方程将包括电感L、电容C、输入电压Vin、输出电压Vout以及占空比D等参数。

平均化处理：由于开关频率远高于输出频率，可以对开关周期内的变量进行平均化处理，得到平均电感电流Iavg和平均输出电压Vavg。

这些平均值将用于建立小信号模型。

小信号分析：在平均化的基础上，引入小信号扰动，如ΔD（占空比的小信号变化）、ΔVin（输入电压的小信号变化）等。

通过线性化处理，得到小信号传递函数，用于分析系统的稳定性和动态响应。

平均后的波形在DCM下，平均后的波形主要包括：

Q1两端的电压v：在Q1导通时为Vin，在Q1关断时为0（或接近0，考虑到二极管CR1的导通压降）。

CR1两端的电压：在Q1导通时为0，在Q1关断时为Vout（或Vout加上二极管CR1的导通压降）。

CR1上的电流i：在Q1关断时等于电感电流iL，在Q1导通时为0。

重复用到的关系式，整个开关周期内的终端平均电流由下式给出:

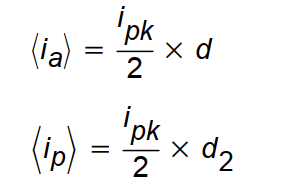
括号里的变量(像<ia>)代表了在整个开关周期内取均值的量。

因为在整个开关周期内，电感上的电压均值为0，下面的电压均值关系成立:

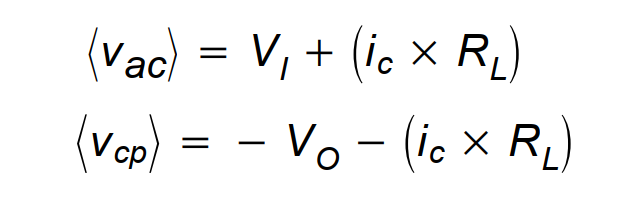
由于i.R,的值相比于V和V,很小，所以在做模型时就忽略了这些值以便方程更容易处理。在时间d xT内，电流i从0值开始，停止于ipk’，因为在这段时间内电感上的电压是常数，且有V=〈v。〉，所以有下式成立:

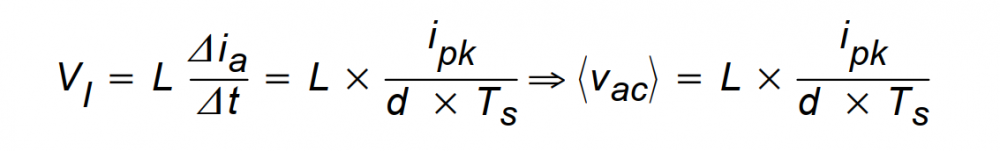
类似的，在时间d2 xT、内，电流ia从i值开始，停止于0，同样因为在这段时间内电感上的电压是Vo=〈v)，所以有下式成立:

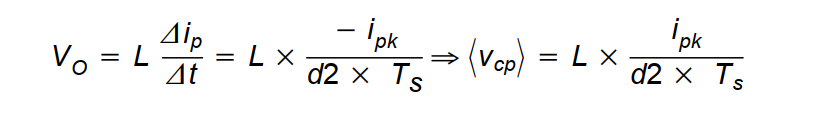
有了上面的四个方程，我们从脉冲宽度调制开关模型的输入边(v边)开始推导。解方程(3)得到i，利用V=〈v〉，然后代入方程(1)就可以得到:

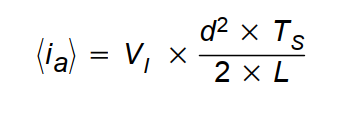
注意到流进终端a的电流均值与输入电压V成正比，有效阻抗定义如下：

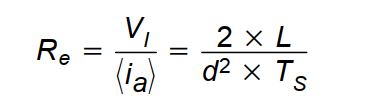
现在我们可以把上面的输入和输出关系应用到等效的电路模型。这个模型在确定功率源的直流工作点很有用。输入端口可以简化模型为电阻R。，输出端口简化为一个从属的功率源，这个功率源输送的功率等于输入电阻R,消耗的功率。这个等效电路的构成见图所示。.

非连续导通模式脉冲宽度调制开关模型：

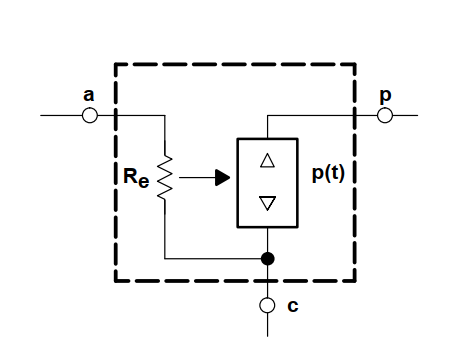
为了用这个模型来描述非连续导通模式下功率级的稳态分析，我们研究这种buck-boost转换器。这个分析过程跟之前的连续导通模式(CCM)是一样的，等效电路带进原始电路，电感看作是短路，电容看作是断路。非连续导通模式下的buck-boost转换器的原理图如图所示。

非连续导通模式下的buck-boost转换器原理图：

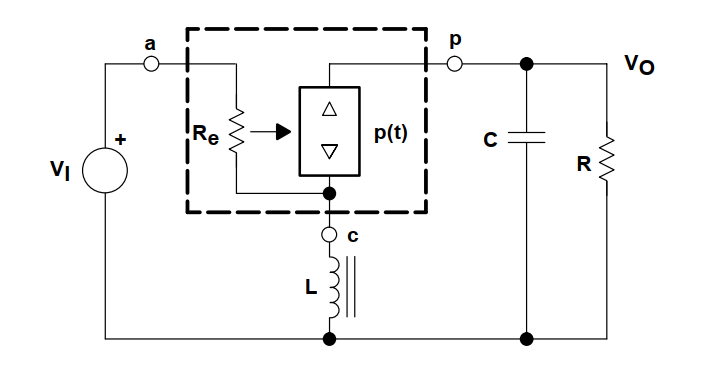
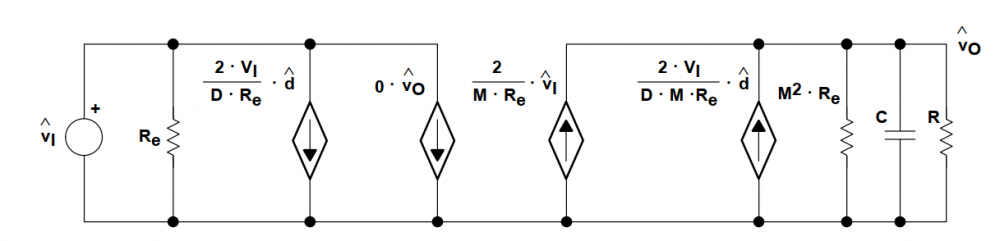
现在为了推导小信号模型，跟在连续导通模式(CCM)中的推导过程一样，扰动图12中的电路，并线性化，想了解推导的详细过程，读者可以参考中的细节。这个工作在非连续导通模式下buck-boost功率级的小信号模型如图所示。

非连续导通模式下buck-boost功率级的小信号模型：

总结：

Buck-Boost转换器在非连续导通模式（DCM）下的小信号分析。DCM与连续导通模式（CCM）的主要区别在于，DCM中开关器件和输出二极管在每个周期内只会导通一次。因此，DCM下的小信号模型与CCM有很大的不同。文章通过定义开关周期和占空比、分析开关动作、建立状态空间方程、平均化处理和小信号分析等步骤，推导了Buck-Boost功率级DCM下的脉冲宽度调制开关模型。在DCM下，平均后的波形包括Q1两端的电压、CR1两端的电压和CR1上的电流等。通过解方程和代入关系式，得到了输入和输出之间的关系，并定义了有效阻抗。文章将输入和输出关系应用到等效的电路模型中，得到了非连续导通模式下Buck-Boost功率级的小信号模型。