EEPW论坛

如图1所示，我们可以看到一个振荡器，具体来说是一个Colpitts振荡器（考毕兹振荡器）。

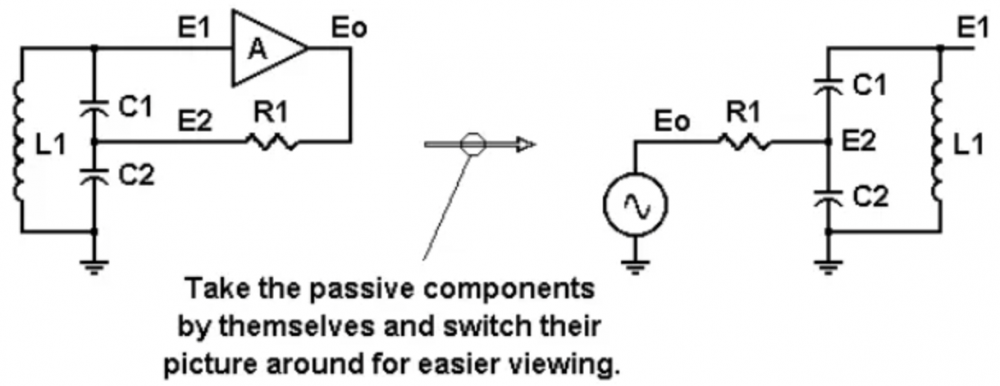
图1：Colpitts振荡器，其中无源元件排列在右侧，以便于查看

有一个由无源元件和有源增益模块组成的RLC网络。就此模型而言，增益模块的输入阻抗足够高，以至于可以忽略其负载效应，增益模块的输出阻抗为零，其增益值A名义上为1，或者可能略小于1。电阻R1模拟了真实世界中增益模块可能存在的输出阻抗。

为了分析该电路，我们取无源元件，将其重新绘制在右侧，然后开始使用节点分析(图2)项G1=1/R1和项S=j/(2*π*F)。

图2：用于图1右侧电路的节点分析

得到了Eo和E1之间的关系(排除E2)后，我们执行几个代数步骤将该关系转化为有用的形式，如图3所示。

图3：代数重排使传递函数变为更有用的形式

注意，最后一个方程的分母是三次多项式。它是一个三阶多项式，因为电路中有三个独立的电抗元件，L1、C1和C2。

还请注意，多项式的阶数必须与电路中独立电抗元件的数量相匹配。如果我们得出其他阶数的代数表达式，那么我们肯定在某个地方犯了错误。

绘制E1/Eo比率与频率的关系图，我们在图4中看到以下情况。

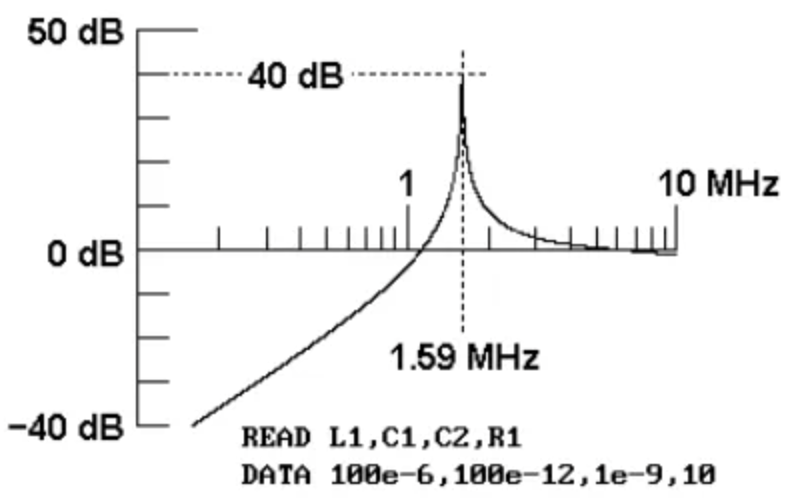
图4：图3中代数分析得出的E1/Eo与频率的关系图

无源RLC网络的传递函数在1.59MHz频率处出现一个明显的峰值。当我们对该传递函数运行SPICE仿真时，我们发现了相同的结果(图5)。

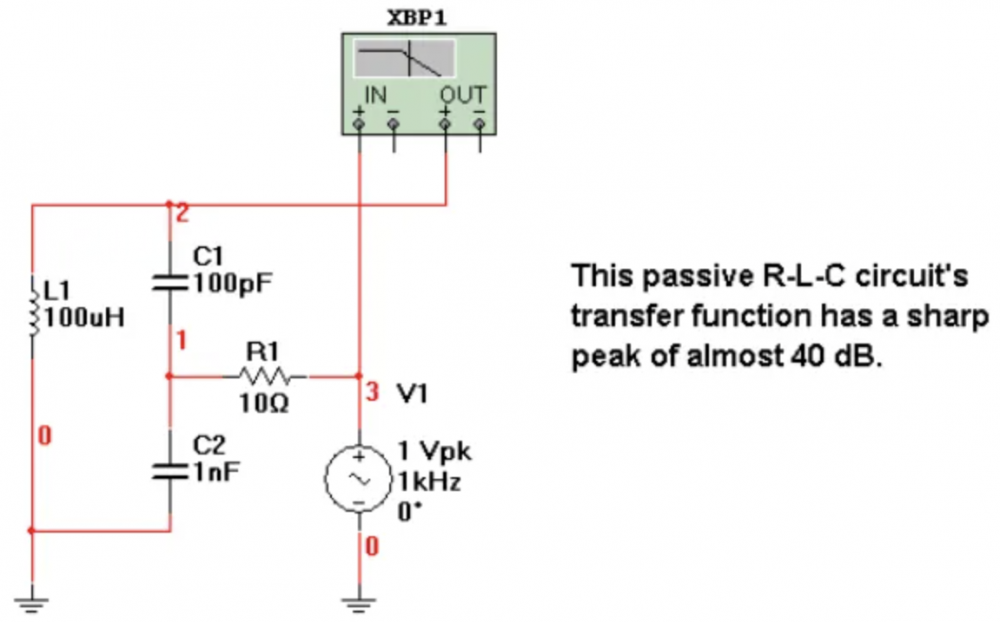
图5：无源RLC网络的SPICE分析显示E1/Eo与频率的关系，在1.59MHz处具有接近40dB的明确峰值

当我们让增益模块成为一个电压跟随器(如图6所示的JFET源极跟随器)时，我们会看到非常接近该传递函数峰值频率的振荡。

图6：通过引入JFET源极跟随器由图5所示的无源网络构建而成的Colpitts振荡器，该振荡器反映了传递函数峰值的频率