EEPW论坛

本文介绍了MOSFET中的噪声机理及其测试与建模方法。

在无线通信中，接收器接收到的信号非常小，以至于系统中只能容忍有限的噪声。因此，对于电路设计人员来说，能够以合理的精度预测MOS器件的噪声以及了解噪声对器件几何和偏置条件的依赖是非常重要的。因此，精确的器件模型应该包含噪声模型，能够准确地预测器件的噪声行为。这篇我们来聊一聊器件噪声模型。

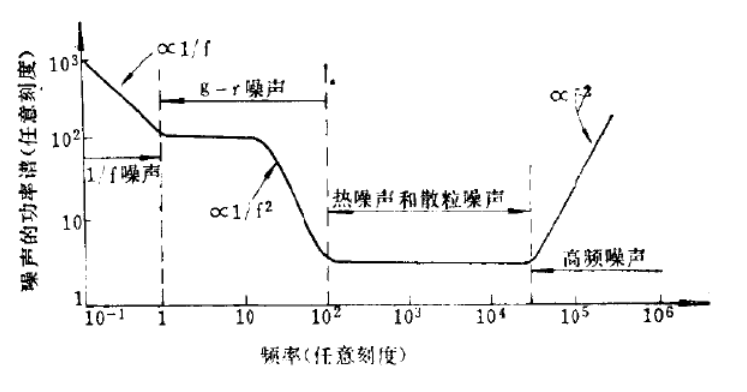
常见的器件的噪声按照物理机制的不同分类如下图所示，分为：散粒噪声，闪烁(1/f)噪声，热噪声，产生-复合(g-r)噪声四大类。在一般的频率范围内，热噪声和散粒噪声的功率谱密度与频率无关，统称为白噪声。1/f噪声和g-r噪声的功率谱密度与频率相关，前者与1/f成正比，后者则按1/(1+f^2/f0^2)规律变化，其中f0为转折频率，统称为有色噪声。由于这两种噪声在低频情况下显著，也成为低频噪声。在很高的频率下(如大于1GHz)，热噪声和散粒噪声也将随频率变化。当频率接近于器件的高频截止频率时，噪声随频率的增加而上升往往不是因为出现了新的噪声机制，而是由于器件的增益随频率下降所致。噪声问题，包括它的SPICE模型，在过去的几十年里得到了广泛的研究。后面我将以BSIM4中的1/f Noise Model和Thermal Noise Model来和大家做一些讨论。

要研究噪声，我们需要引入几个概念，以方便大家理解。

相关性函数与功率谱密度（Power Spectral Density，PSD）

统计平均量

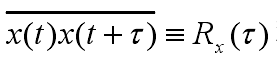
称为随机变量 x 的自相关函数。它是 t 时刻的随机量数值在此时刻后能够持续多长时间的度量，反映了随机量在不同时刻数值之间的相关性。

设x(t)为一个平稳随机变量，则x(t)的功率谱密度定义为:

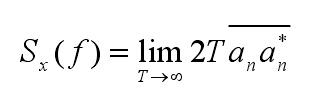
式中，f 为频率；an 为x(t)在时间区间 0≤t≤T 内的傅里叶展开系数，an*表示an的复数共轭值。

根据维纳—辛钦(Wiener—Khintchine)定理，随机变量x(t)的自相关函数Rx(t)与功率谱密度Sx(f)之间满足下列关系:

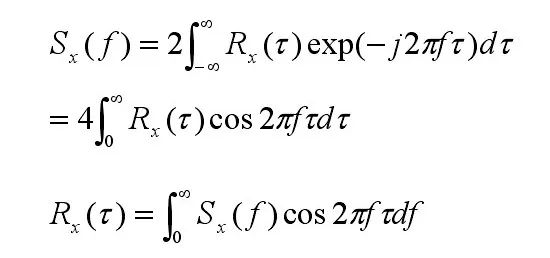
也就是说，Sx(f)是2Rx(t)的傅里叶变换，Rx(t)是Sx(f)/2的傅里叶逆变换。 根据Rx(t)的定义，令上式中的τ =0，得：

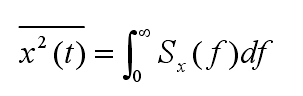
可见，Sx(f)的物理意义是在频率 f 附近单位频宽内起伏量 x 的均方值。Sx(f)随频率 f 变化的曲线就是通常所说的噪声频谱。它表示x(t)在频率域的统计量，表示了随机信号的各个频率分量所包含的强度。

二端口网络的噪声理论和参数表示

在更一般的表述中，MOSFET晶体管可以用如下图所示的产生噪声的二端口有源网络来描述。在该图中，网络的输入输出导纳Yi和Yo均为复数。例如，Yi = Gi +jBi，Gi为电导，Bi为电纳。

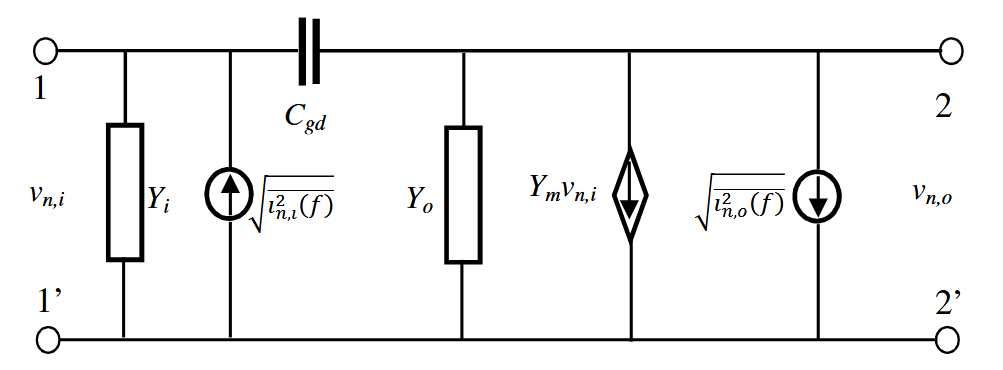
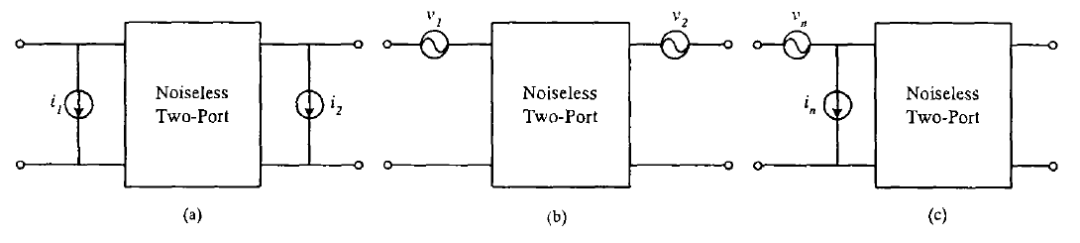
任何二端口噪声网络均可以用一个相应的无噪二端口网络与两个外加的噪声源构成的等效电路来表示。根据噪声源的不同组合，这种等效电路有六种不同的表征方法，但是在实际应用中，如下所示，(a)导纳表征、(b)阻抗表征和(c)ABCD参数表征是最为常用的。

每种表征方式中的噪声特性均可以采用相关矩阵C来表示，矩阵中的每个元素，即功率谱Cs1s2*代表的是噪声源s1和s2之间的自相关和互相关函数的傅立叶变换，其定义如下：

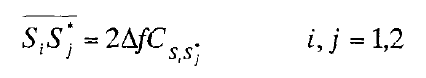
上式中，左边是噪声功率谱密度，右边是噪声相关矩阵。上述三种不同表征的噪声等效网络表示如下，且它们之间是可以相互转化的。

导纳表征

这种表征方式通常在两个二端口噪声网络并行连接的情况下使用，设两个并联网络为Y1和Y2，则具体表示如下：

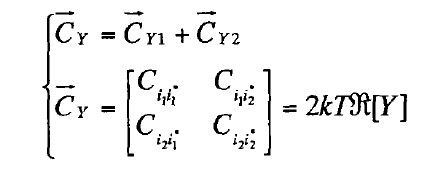
式中，Cimin表示的是输入端、输出到噪声电流的自噪声功率谱密度和互噪声功率谱密度；R[Y]代表的是无源网络的参数实部。

阻抗表征

这种表征方式通常在两个二端口噪声网络串行连接的情况下使用，设两个并联网络为Z1和Z2，则具体表示如下：

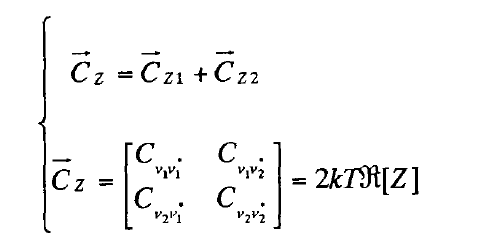
ABCD参数表征

这种表征方式通常在两个二端口噪声网络级联的情况下使用，设两个并联网络为A1和A2，则具体表示如下：

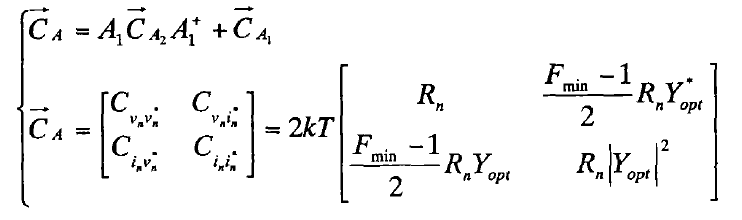
式中，A1*表示的是A1矩阵的转置共轭矩阵，相关矩阵中的每一个元素均可以从所测试的噪声数据中得到(Rn, Fmin, Yopt)，这种表征方法在实际电路噪声分析中最为常用。

三种不同表征方法之间是可以相互转换的，具体如下表所示：

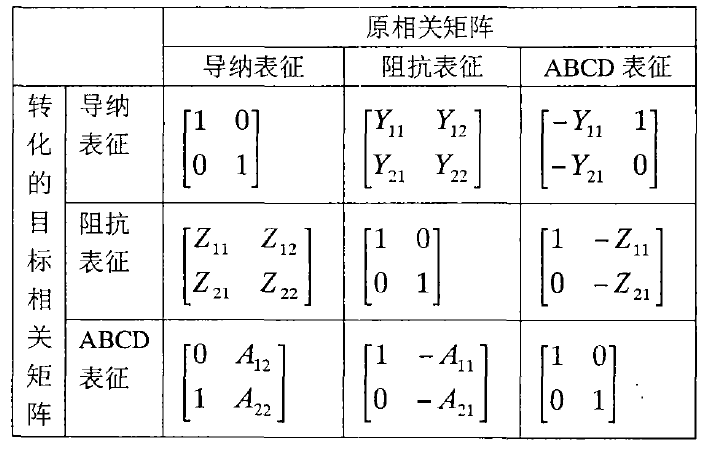
噪声的四个参数表示

一个系统的噪声系数大小不仅仅取决于系统内部产生的噪声,还与驱动该系统的源导纳或源反射系数有关，如下图所示是系统噪声系数与源反射系数之间典型的抛物线关系，图中x轴、y轴分别是源反射系数的实部和虚部，z轴是系统在一定源反射系数下的噪声系数。它们之间的这一关系可以采用经典的四个噪声参数Fmin, Rn, Gopt, Bopt表示:

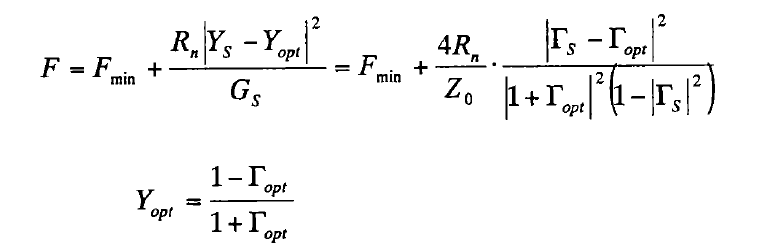
噪声因子（F）：是最常用的噪声参数，它描述了二端口网络对输入噪声的放大或衰减程度。噪声因子是网络输出端信噪比与输入端信噪比的比值，即F=SNRout/SNRin。

最小噪声因子（Fmin）：二端口网络能达到的最小噪声因子。

噪声系数（NF）：与噪声因子类似，也是描述二端口网络噪声性能的参数，通常以分贝（dB）为单位表示，NF=NFmin+matched network factor。

噪声温度（T）：与噪声因子类似，也是描述二端口网络噪声性能的一个参数。它将网络的噪声水平与一个假想的绝对温度相联系，定义为在相同带宽下，等效噪声功率与绝对温度的比值，即Tnoise=Pnoise/kΔf。

等效噪声电阻（Rn）：表征二端口网络噪声源的一种方式，它假设网络的噪声由输入端的一个等效电阻产生，计算公式为Rn=Pnoise/kTB。

最佳源反射系数（Γopt）：当信号源的反射系数为此值时，二端口网络达到最小噪声因子。

闪烁(1/f)噪声

闪烁噪声通常又被称为低频噪声或 1/f 噪声。凡是功率谱密度与频率成反比的随机涨落现象均可称为 1/f 噪声。在电子器件中 1/f 噪声的电压功率谱密度可以写成如下的形式：

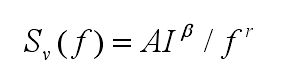
其中，I 为通过器件的电流，f 为频率，参数 A 由器件结构等特性决定，r 可取 0.8～1.2，对于均匀材料，β=2.0。

1/f噪声则与器件中的电流或外加电压有关，一旦电流或电压消失，这些噪声也就不复存在。

闪烁(1/f)测量：

虽然通过对直流数据进行傅里叶变换，随着时间的推移进行采样，任何直流测量系统都可以对噪声进行表征。如下图是一个BJT直流采样后通过FFT变换，可以得到Noise的特性。但是这种方法受诸多因素限制，如，DC偏置的影响，采样的限制，系统噪声，连线的影响，环境的影响。测得的噪声数据波动大，数据处理麻烦，难以复现。

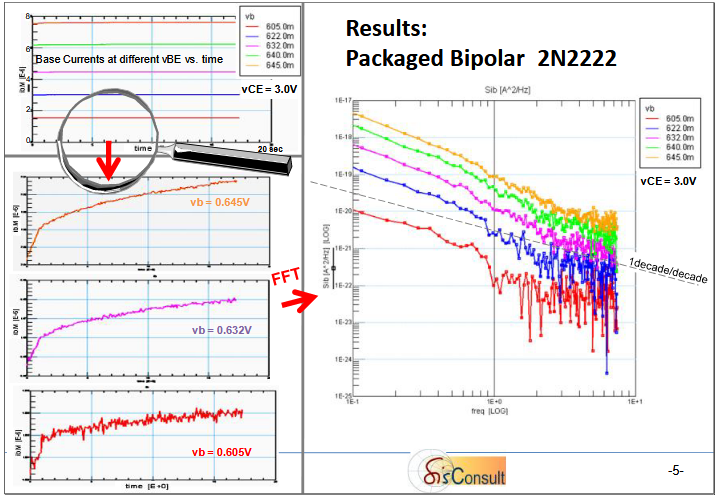
因此业界提出了一些集成方案和设备。

1/f噪声模型：

对 1/f 噪声的研究有两种物理模型，一是表面载流子涨落模型，二是迁移率涨落模型。

McWhorter 模型认为闪烁噪声来自于靠近 Si-SiO2界面的氧化物陷阱对载流子的俘获和释放

Hooge 模型认为闪烁噪声来自于载流子-声子散射引起的迁移率波动。

在BSIM4模型中提供了两种1/f噪声模型，它们可以通过指定BSIM4噪声模型flag参数FNOIMOD进行选择。 FNOIMOD=0

当FOIMOD设为0时，调用SPICE2g6 ，SPICE3和BSIM3v3中的一个简单的、经验的闪烁噪声模型。该模型便于手工计算。该模型计算出以方安培每赫兹为单位测量的1/f噪声功率谱密度为：

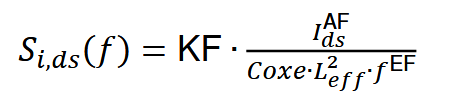
式中：KF为1/f噪声系数，默认值为0.0；AF为沟道电流的指数，EF为频率指数，无量纲化后的AF和EF默认值均设为1.0。所有这些参数都是通过拟合实测闪变噪声数据提取的；Coxe是电栅介质的单位面积电容。

FNOIMOD=1

当FNOIMOD设置为1 (默认选项)时，将采用基于物理的、统一的闪烁噪声模型(将电荷数波动和迁移率波动结合成更一般的理论)。该模型的噪声功率谱密度为：

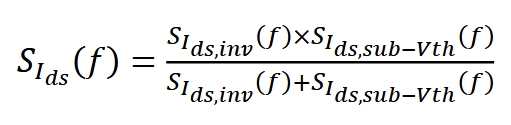
强反型区：

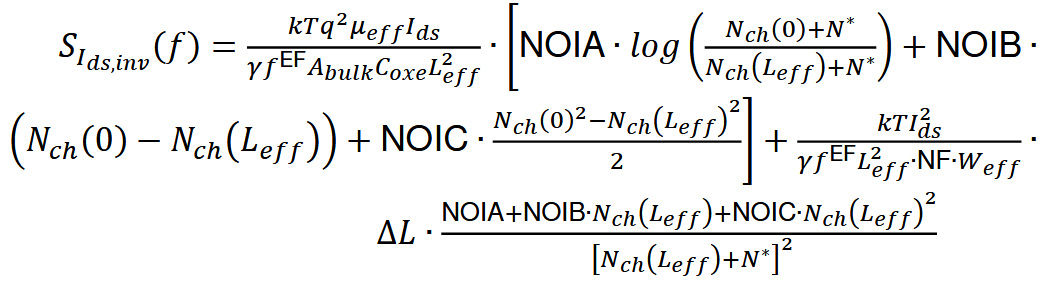
亚阈值区：

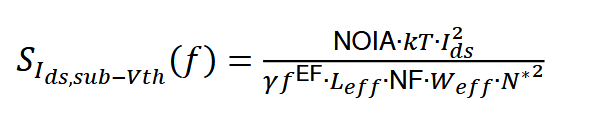
1/f模型提取

低频噪声参数提取，可以在MBP或者ICCAP中实现。如果要在ICCAP中实现，需要在Test Circuit中定义Noise Circuit。具体会根据调用的仿真器不同有所差异。

ICCAP调用ADS建模

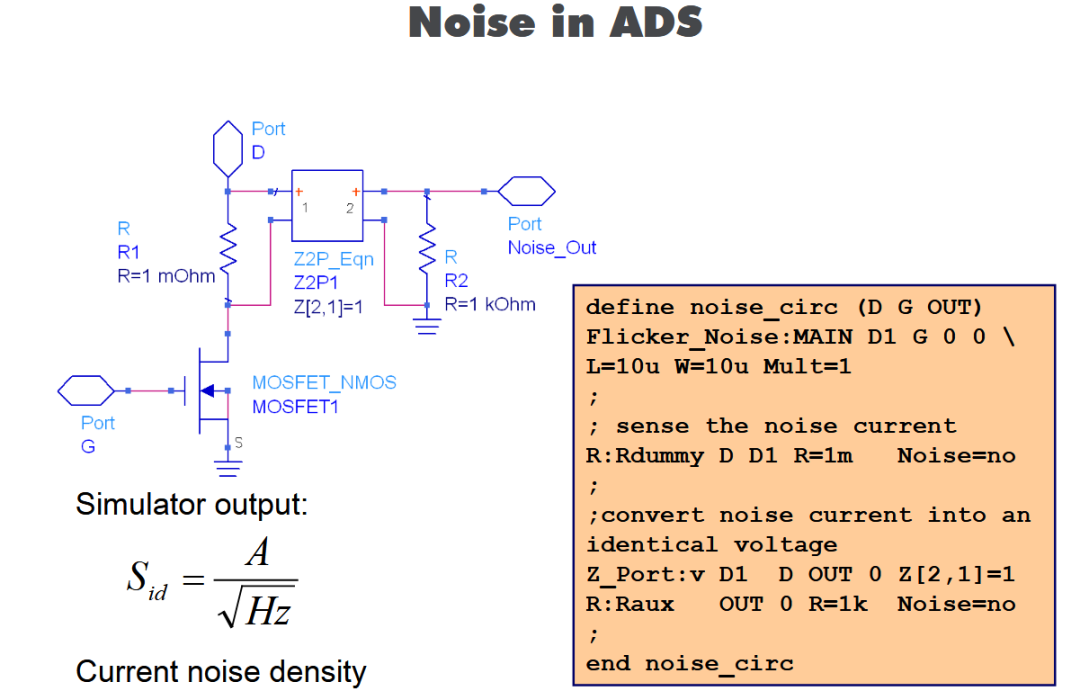
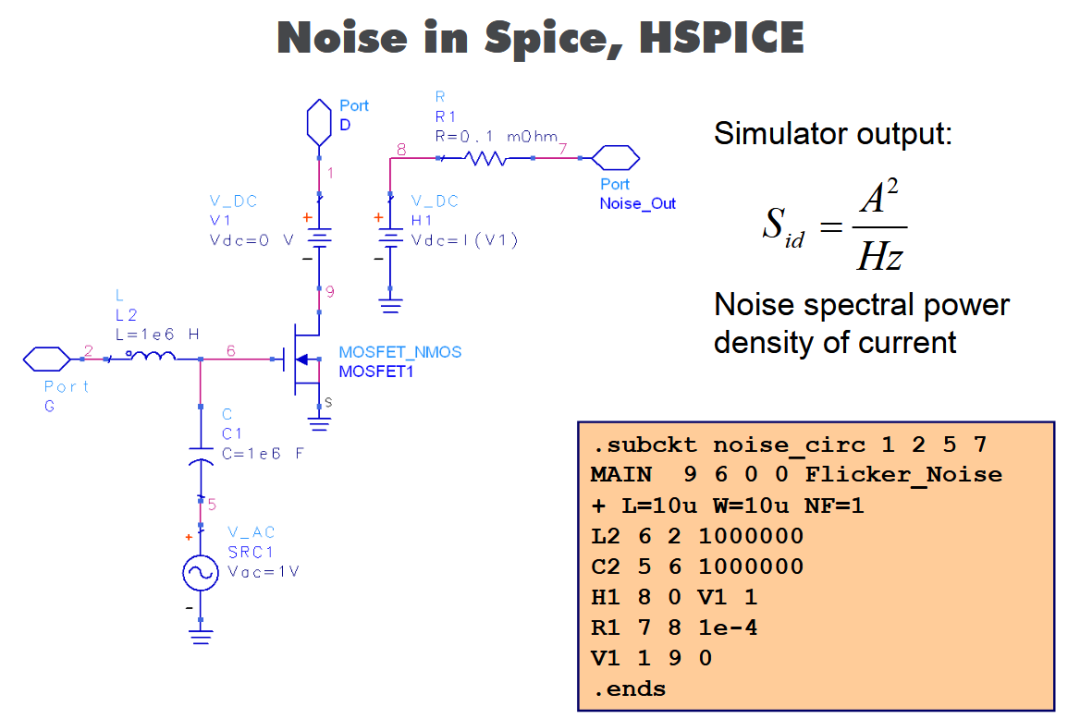
ICCAP调用SPICE，HSPICE建模

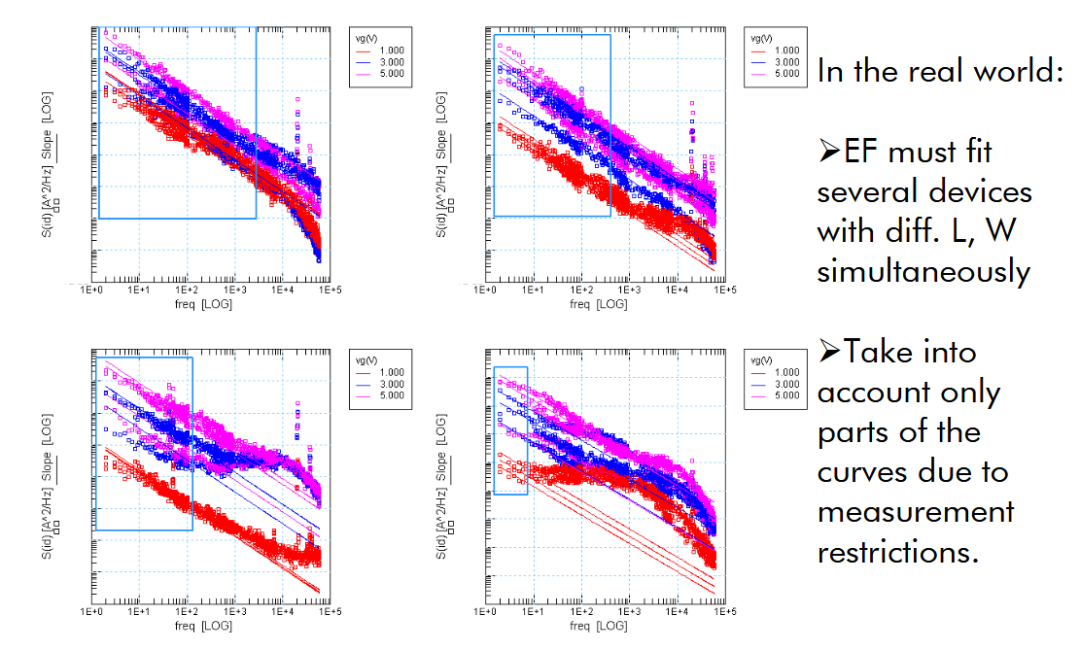
ICCAP中绘制不同尺寸，偏置下的plots进行参数优化拟合。尽量关注log-log坐标轴下线性部分。注意仿真与测试单位要统一。

热噪声

由于闪烁噪声会随频率的增加而衰减，因此在微波频率下它变得微不足道。当器件的工作频率高于转角频率（corner frequency，在转角频率处沟道热噪声与闪烁噪声大小相等）时，产生于 MOSFET 器件沟道的热噪声成为器件的一个主要的噪声源，热噪声也被称为沟道热噪声。热噪声起源于晶体中载流子的随机热运动，广泛存在于各种电阻性元器件之中。热噪声的电压和电流的功率谱密度分别为：

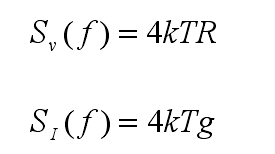
由此可以看出，热噪声的大小只与电阻和温度有关。

噪声参数测量：

从噪声参数的表达式可以看出，其噪声参数是一个与源阻抗相关的一个函数，其中又包括，最小噪声系数，等效电阻和最优源阻抗的幅度和相位，总共4个系数，为四元一次方程，因此，理论上需要4个源阻抗即可解出这个函数。但是，实际上4个源阻抗是远远不够的。因为有可能在某些源阻抗下无解。

Focus微波噪声参数测量系统为提取待测器件( DUT )的准确噪声参数提供了解决方案：最小噪声系数、等效噪声电阻和最佳噪声反射因子( Gamma和Phase)。如下图所示，该噪声测量系统利用Keysight的PNA-X，主要包括3个部分：输入噪声模块( INM )、输出噪声模块( ONM )和噪声模块控制器( NMC )。这些模块的设计在提高噪声接收器精度和灵敏度的同时，也简化了系统标定和DUT测量过程，被业界广泛使用。具体测试方法请参考其手册。

沟道热噪声模型

在MOSFET热模型中，热模型的研究有很多，但都有一个共同点就是将沟道当作一个独立的电阻处理，尽管它不是欧姆的。在BSIM4模型中提供了两种热噪声模型，它们可以通过指定BSIM4噪声模型flag参数TNOIMOD进行选择。

TNOIMOD = 0

这是BSIM4默认的沟道热噪声模型，它是基于电荷的模型。背后的原理其实很简单，沟道电阻就是将沟道的反型层电荷从源端积分到漏端。

沟道电流：

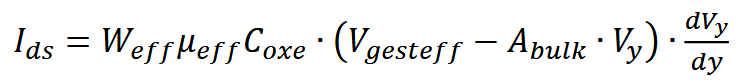
沟道电阻的微分形式：

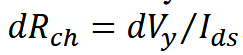
积分后可得到：

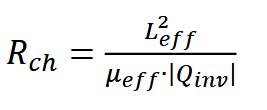
考虑到串联的LDD电阻后，沟道热噪声功率谱密度为：

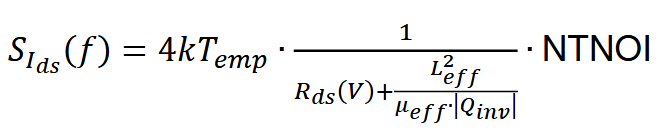
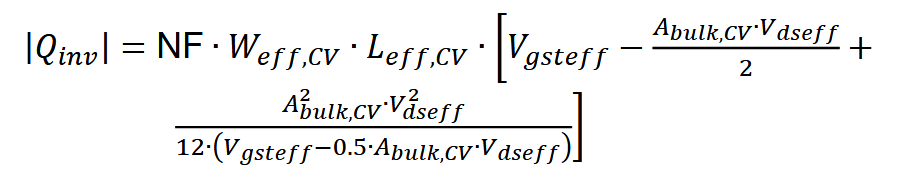
式中，NTNOI引入是为了模型的灵活性和精度，默认值为1；只有当RDSMOD=0时，LDD电阻的噪声在上式中考虑，RDSMOD=1时，热噪声被单独的Rd, Rs电阻考虑，Sr(f) = 4kTemp.R。

这一模型适用于工作在线性区的长沟道器件。其次，现在将沟道电阻处理为常规电阻。

TNOIMOD = 1

在GHz范围内，MOSFET沟道必须考虑为一系列沿沟道平行于y轴的分布RC段，如下图所示。分布栅电容表示电容耦合。每个电阻段Rch,y产生一个热噪声电压∆vdy，可被该段( gdy , gmy和gmby)特有的漏极电导和栅体跨导调制，从而在漏极处产生一个噪声电流∆idy。该沟道噪声电流的很大一部分可以在GHz频率下流入栅极和外电路，产生栅极噪声电流ig，从而产生栅极噪声电压vg。这种栅极噪声被称为诱导栅极噪声。

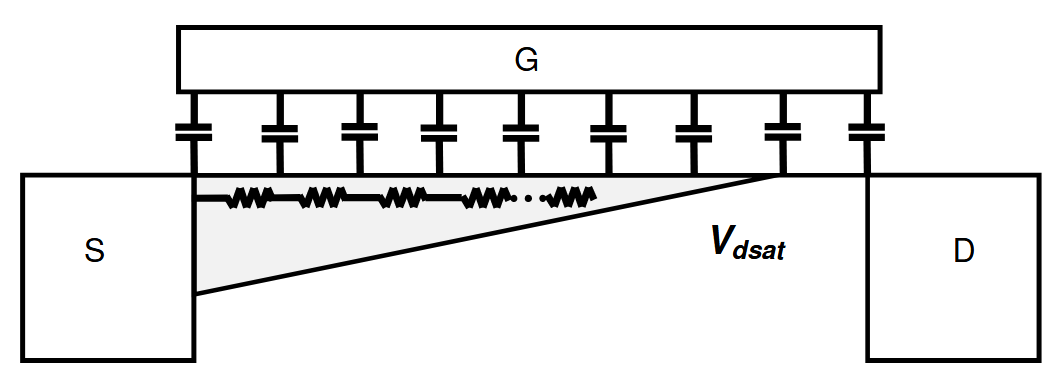
BSIM4中采用了噪声分割的方法，将总量拆分为如下图所示的两部分：一部分认为在沟道外部，而另一部分仍然在沟道内部。噪声分割的目的是通过沟道和栅极之间的分布式RC网络来建模诱导的栅极噪声电流。

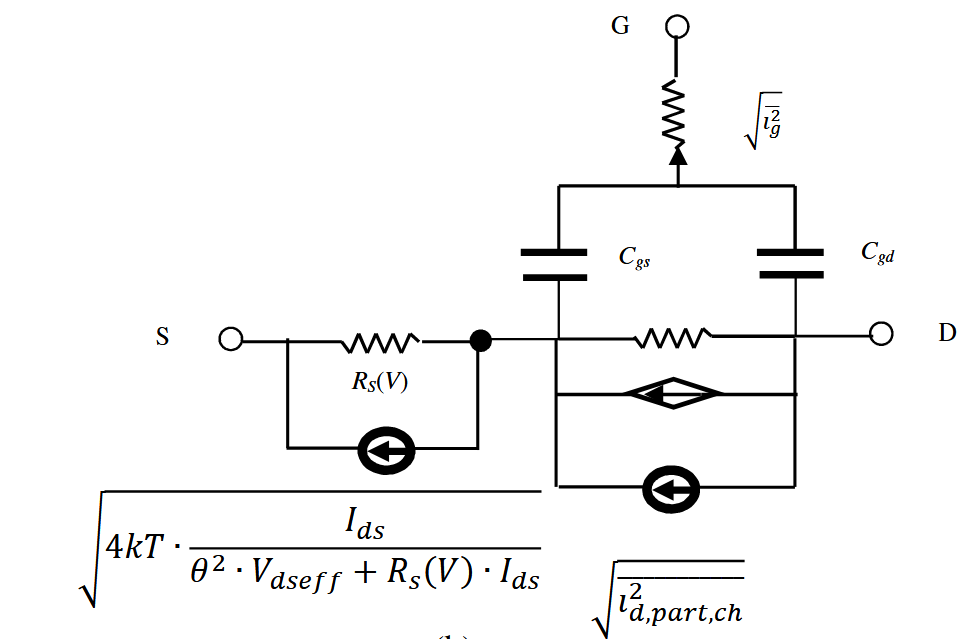
漏极总的噪声电流功率为：

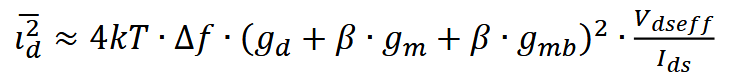
式中，β称为有效跨导放大系数。

栅极噪声电流功率为：

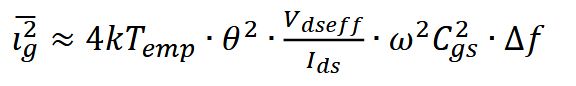
式中，θ为噪声分割系数。

噪声源分割到源侧引起的漏极噪声电流功率为：

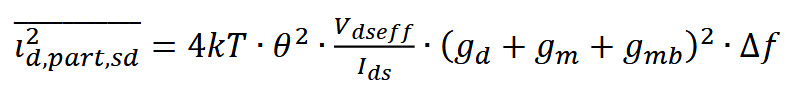
本征沟道区漏极噪声电流功率为：

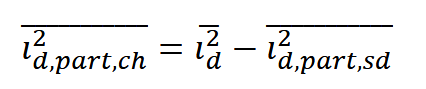
β和θ的表达式为：

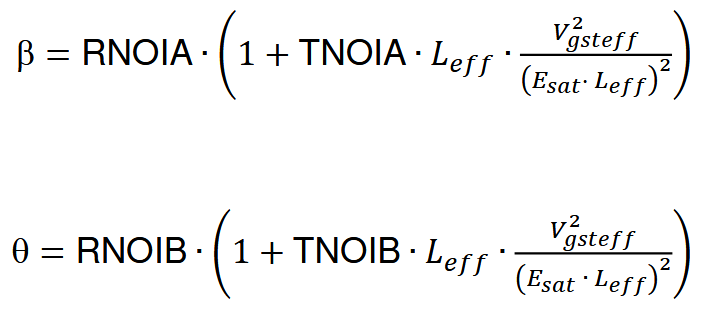
热噪声参数提取：

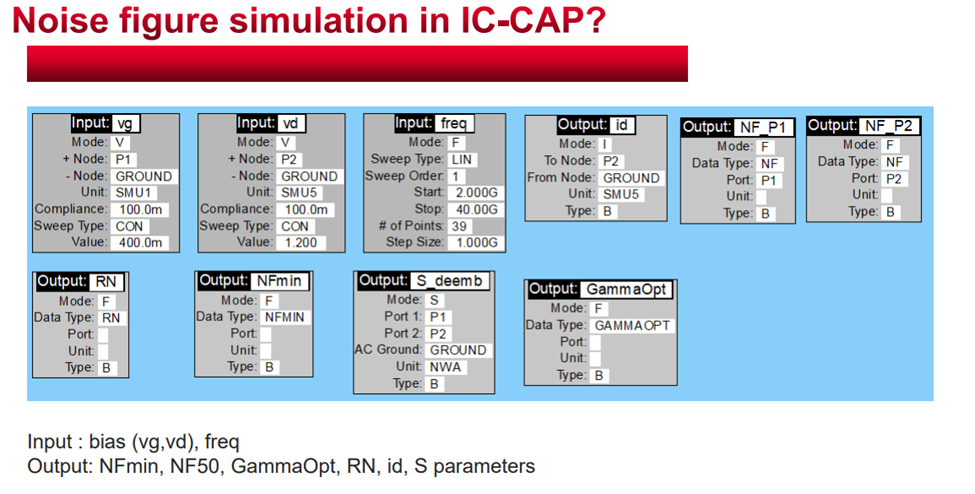
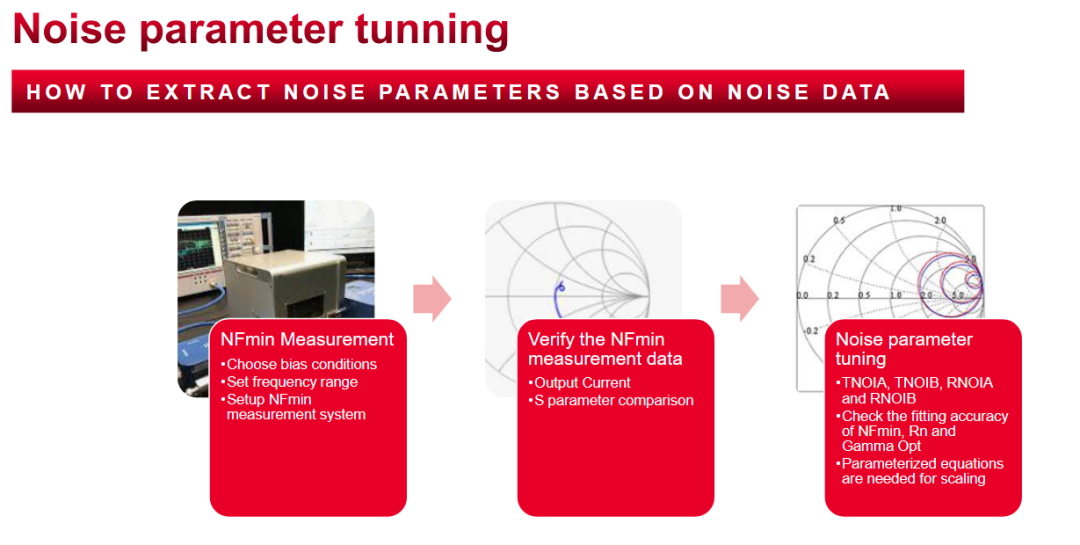
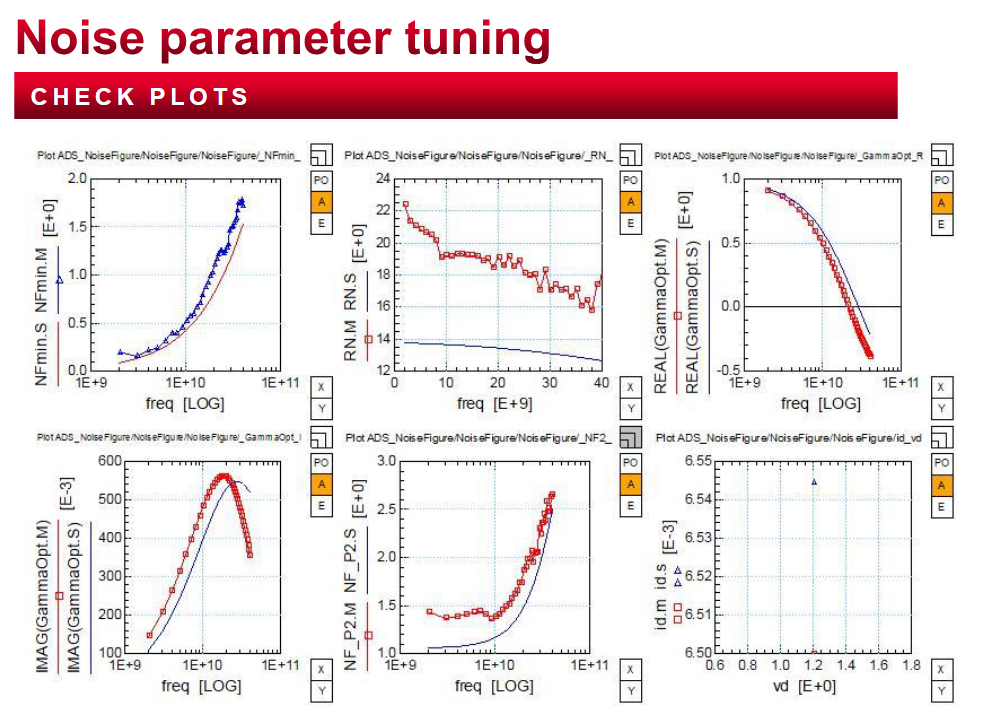
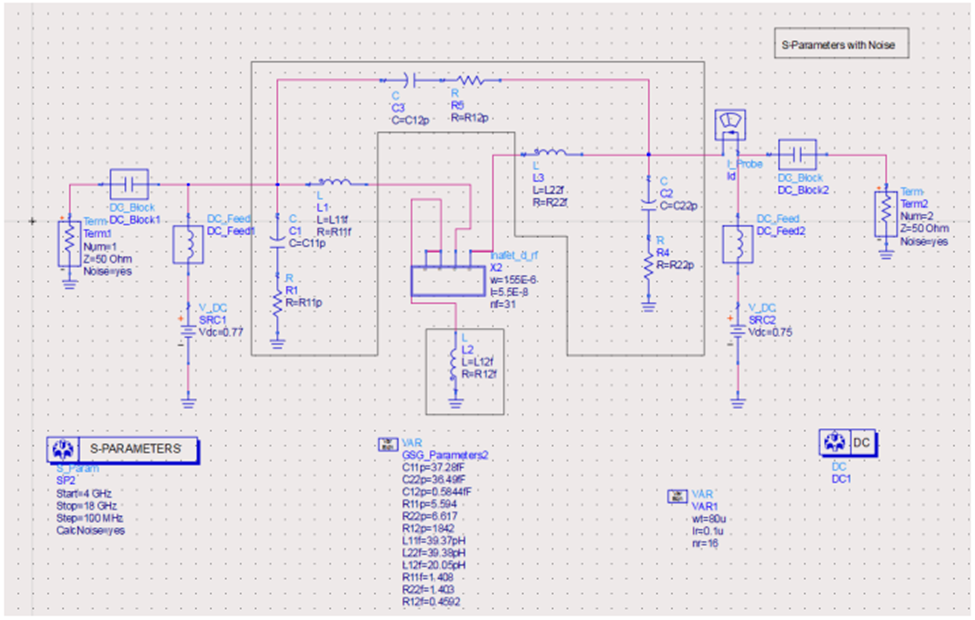
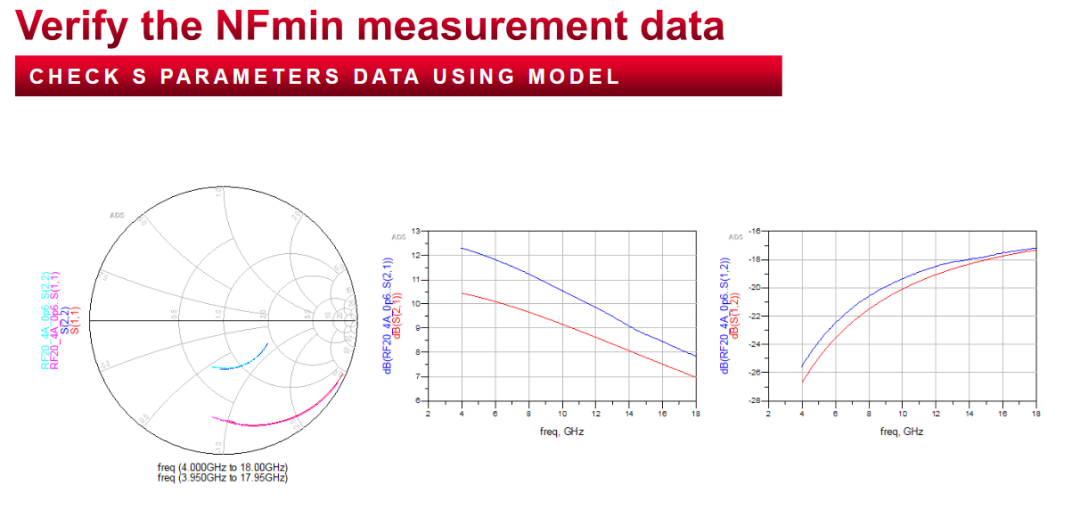
ADS原理图验证： 从下图可以看到，NFmin的仿真环境比较简单，主要包含有两个端口的Term(分别为50ohm)，以及G和D两端的bias，外围PAD的等效部分(这部分会影响最终的NFmin的仿真结果，model release之后的结果是不带有pad这部分的)，以及S参数的仿真条件设置(主要就是起始频率，终止频率，步长，还有注意要勾选Calculate noise)。