EEPW论坛

在模拟集成电路设计中，精确的MOSFET模型是确保电路性能预测准确性的基石。而沟道电荷分配原则，正是连接晶体管直流特性与交流特性的关键桥梁。如果简单地认为所有电荷都均匀分配或不随偏置变化，就会严重错误地估计电路的速度（fT）、延时和AC特性。今天，我们将从物理本质出发，深入解析这一重要概念。

为什么需要关注沟道电荷分配？

简单来说：沟道电荷的分配方式直接决定了MOSFET的本征电容特性。

当我们分析电路的高频性能、开关速度或稳定性时，晶体管的电容参数(Cgs、Cgd、Cgb等)起着决定性作用。这些电容并非固定值，而是随着偏置电压剧烈变化的非线性元件。 传统的简单模型认为沟道电荷均匀分布，但这与物理现实相去甚远。

实际上：

在线性区(Vds很小)，沟道电荷近似均匀分布

在饱和区(Vds > Vdsat)，沟道在漏端夹断，电荷分布极度不均匀

在亚阈值区，电荷分布又呈现不同的特征

如果忽略这种非均匀性，将严重误判电路性能!

沟道电荷分配的物理本质

理论基础：Ward-Dutton电荷分配模型 1978年，Ward和Dutton提出了奠基性的电荷导向模型。其核心思想是：基于电荷守恒原则，将总沟道电荷合理地"分配"到器件的四个端口（栅、源、漏、体）。

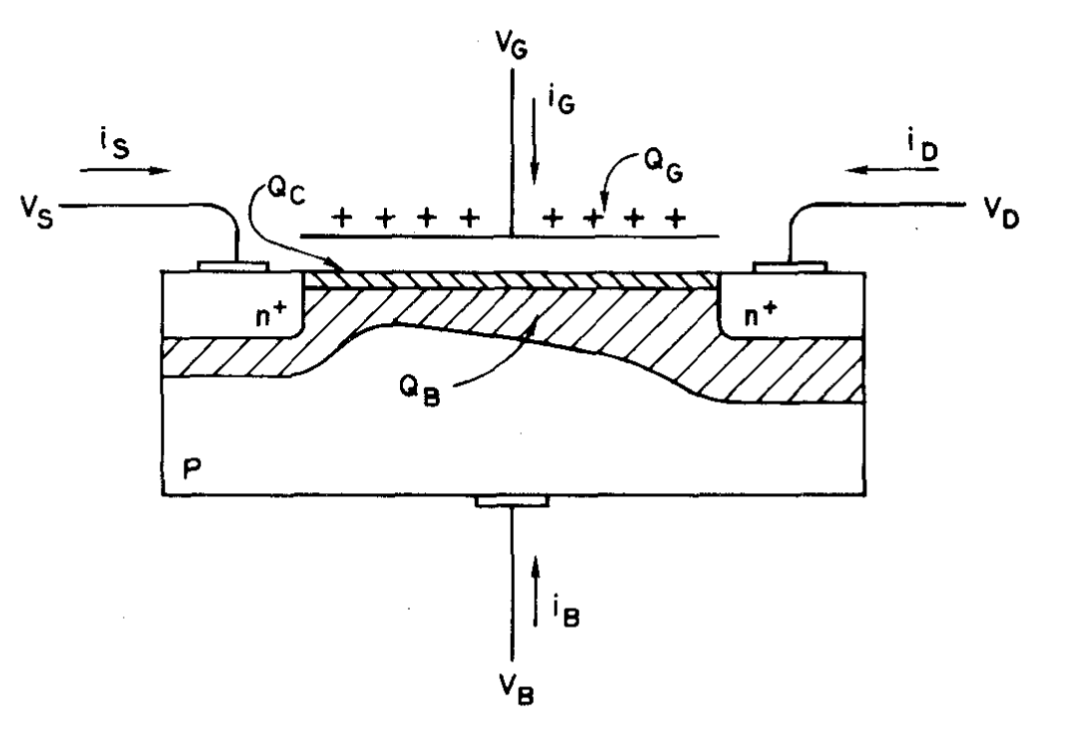
图1：电荷导向模型 电荷导向模型：

所提出的模型基于MOS结构中的实际电荷分布（如图1所示）。对于任何空间区域，我们可以写：

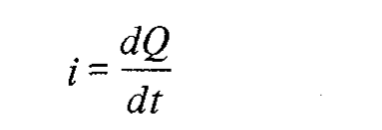
其中 i 是流入该区域的净电流，Q 是该区域中包含的总电荷。因此，我们可以写：

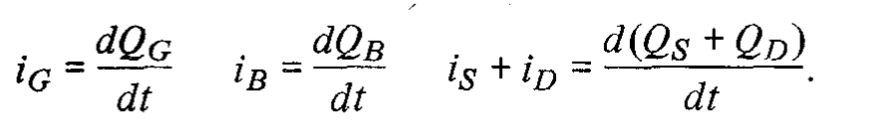
电荷守恒方程： QG+QS+QD+QB=0 其中总沟道电荷 QC可表示为：

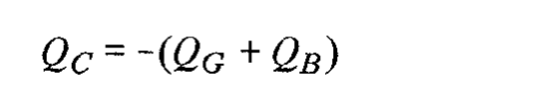
并且与源电荷和漏电荷有关：

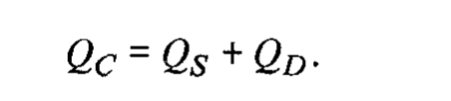
不幸的是，漏极和源极电荷的定义不如栅极和体电荷，必须通过分配通道电荷来获得。因此，我们必须有一个将Qc划分为QD和QS的算法。这种拆分可以通过多种方式完成。

1. 物理分割

将沟道按照沟道中的某一点y0分割，y0=a*L，L是沟道长度，因此可以按照如下方式分配：

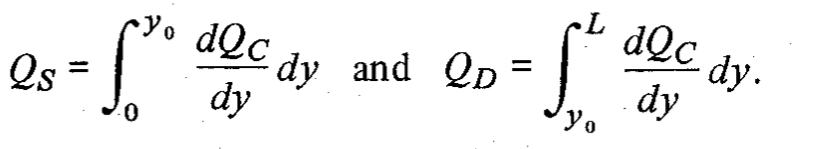
2. 数学分配

数学分配中，QD = b*Qc, QS = (1 - b)*Qc，其中0 <= b <= 1。通常，b 可能是端子电压的函数。

在线性区，虽然沟道均匀，但载流子从源端注入，导致源端"感应"到更多电荷。在饱和区，沟道在漏端夹断，几乎没有电荷归属于漏端，大部分电荷聚集在源端附近。通过理论推导和实验验证，我们得到了两个经典分配规则：

线性区(40/60规则)：

a) 漏端电荷 Qd ≈ 40% QI

b) 源端电荷 Qs ≈ 60% QI 饱和区(0/67规则)：

a) 漏端电荷 Qd ≈ 0% QI b) 源端电荷 Qs ≈ 67% QI

c) 栅端电荷 Qg ≈ 33% QI

从理论到实践：连续可微的分配函数

Tsividis的平滑过渡方案 经典的40/60和0/67规则只是两个极端情况。在实际电路中，晶体管工作在连续的偏置范围内，我们需要平滑的过渡函数。以BSIM3V3模型为例，我们简单了解一下工程中是如何实现的。 BSIM3v3 将衬底电荷 Qbulk和反型层电荷 Qinv分开处理。总栅电荷 Qg满足电荷守恒方程：

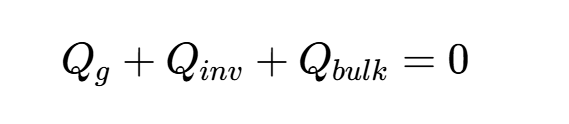
BSIM3v3 手册中详细描述了如何通过一个平滑函数将工作区域划分为三个部分，并对沟道电荷进行分配。模型通过一个关键参数Vgsteff（有效的栅电压过驱动）来平滑连接亚阈值区和强反型区。同时，通过另一个参数Vdseff（有效的漏源电压）来平滑连接线性区和饱和区。

// *** BSIM3v3 电荷模型 Verilog-A 实现 ， 部分代码 ****//


// 电荷计算核心函数
//==================================================================
functioncalculate_charges;
  input Vgsteff, Vdseff, Vdsat, Abulk, Cox, W, L;
 realVgsteff, Vdseff, Vdsat, Abulk, Cox, W, L;


 // 电荷变量
 realQinv_total, Qd, Qs, Qg, Qb;
 realx_share;// 电荷分配系数
begin
 // 6. 总反型层电荷计算
  Qinv_total =calculate_Qinv_total(Vgsteff, Vdseff, Vdsat, Abulk, Cox, W, L);


 // 7. 电荷分配系数计算 - Ward-Dutton 方法
  x_share =calculate_charge_partition(Vdseff, Vdsat);


 // 8. 各端口电荷计算
  Qd = x_share * Qinv_total; // 分配到漏端的电荷
  Qs = (1- x_share) * Qinv_total;// 分配到源端的电荷
  Qb =calculate_bulk_charge(Vgsteff, Vbs, Cox, W, L);// 衬底电荷
  Qg = -(Qinv_total + Qb);  // 栅电荷 (电荷守恒)


 // 9. 使用ddt贡献电荷到端口
 I(g,s) <+ ddt(Qg);
    I(d,s) <+ ddt(Qd);
    I(s,d) <+ ddt(Qs); 
    I(b,s) <+ ddt(Qb);


end
endfunction

关键算法解析

1. 两个核心平滑函数

Vgsteff- 亚阈值/强反型平滑过渡：

// Verilog-A 代码
// 使用对数指数函数实现平滑过渡Verilog-A
Vgsteff = Vtm *log(1+exp(Vgst / (n * Vtm)));

Vdseff- 线性区/饱和区平滑过渡：

// Verilog-A 代码
// 使用平方根函数避免导数不连续
Vdseff = Vdsat -0.5* (Vdsat - Vds - delta +sqrt((Vdsat - Vds - delta)^2+4* delta * Vdsat));

2. 电荷分配算法

BSIM3 使用连续的分配系数x_share：

// Verilog-A 代码
// ==================================================================
// 电荷分配系数计算 - BSIM3核心算法
// ==================================================================
function real calculate_charge_partition;
  input Vdseff, Vdsat;
  real Vdseff, Vdsat;
  real x, Fsat, beta;
begin
 if(Vdsat ==0)begin
   x=0.5;// 避免除零
  endelsebegin
   // 饱和因子
    Fsat = Vdseff / Vdsat;
    beta =2.0;// 平滑因子


   // BSIM3 平滑分配函数
   if(Fsat < 0.1) begin
            x = 0.5 * (1 - Fsat/0.2); // 线性区近似
        end else if (Fsat >0.9)begin
     x=0.0;// 深饱和区
    endelsebegin
     // 过渡区平滑函数
      x =0.5* pow(1- Fsat, beta);
    end
 end


 calculate_charge_partition=x;
end
endfunction

总结

沟道电荷分配原则是MOSFET建模从"简单近似"走向"物理精确"的关键一步。从Ward-Dutton的理论奠基，到Tsividis的平滑过渡方案，再到现代SPICE模型的工程实现，这一领域的发展体现了半导体建模的精髓：在物理精确性与计算效率之间寻求最佳平衡。

对于电路设计师而言，理解这一概念不仅有助于选择正确的模型，更能深入理解器件工作的物理本质，从而在电路优化中做出更明智的决策。