EEPW论坛

什么是过采样

图1是维基百科对过采样技术的描述，总结来说就是在信号采集过程中，如果满足奈奎斯特采样定理（采样率大于等于2倍的信号带宽），我们就可以完整的还原信号。过采样其实就是在采样率远大于2倍的信号带宽的情况下进行采样，比如采样率位2Mhz,信号带宽为100Khz,采样率是信号带宽的20倍。通过过采样技术可以提高分辨率和信噪比，还可以有效地避免信号混叠和失真。

图1过采样维基百科

图2是ADC使用过采样技术的原理原理框图，主要的原理是在输入信号的基础上叠加一个噪声信号比如白噪声或者三角波扰动。然后对ADC采样所得的原始数据进行过采样操作输出对应分辨率的ADC数据。

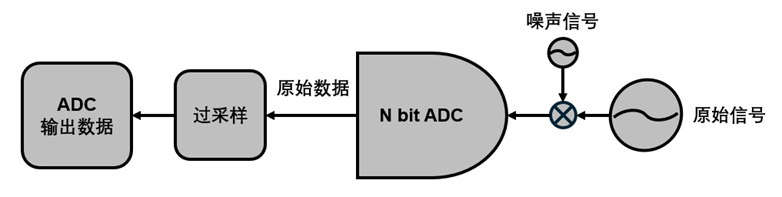
图2过采样原理框图

过采样的工作原理

在进行过采样的原理推导之前我们先需要知道几个ADC动态性能的参数的计算公式。先说信噪比SNR，SNR的计算过程是信号的幅值的均方根（有效值）和噪声幅值的均方根的比，如下式。Srms指的是信号的均方根，Nrms指的是噪声信号的均方根：

对于一个理想的ADC来说，噪声信号理论上只有量化噪声如图3，量化噪声类似于锯齿波或者白噪声。其数学模型可以用下式来表示：

上式中的s表示噪声信号锯齿的斜率，q = Vref/(2^N)。量化噪声的均方根公式可以参考下式：

图3量化噪声图

为什么说当信号带宽远小于1/2采样率的时候会使信噪比SNR提高呢。ADC在采样过程产生的量化噪声可以看作是均匀分布的白噪声，根据上面给的量化噪声的计算公式可以得出总的噪声功率如下：

假设ADC的采样率是Fs,根据奈奎斯特采样定理，噪声均匀的分布在0~Fs/2带宽范围内，可以得到如下噪声的功率密度：

那如果我们把采样率提高N倍，根据奈奎斯特采样定理，噪声均匀的分布在0 ~ N*Fs/2带宽范围内，可以得到噪声的功率密度如下式：

可以看到当采样率变大时，噪声被均匀分布到了更宽的频率范围内导致噪声的有效值减小，被测信号的有效值不变从而使信噪比提高。具体的原理可以参考图4。

图4采样结果FFT图

看到图四大家会不会有这样一个疑问，采样率提高了，是不是意味着噪声分布的频率点也多了呢。总的噪声是所有噪声的和为什么就能确定噪声减小了呢。实际上ADC采样的过程是离散化的，我们对ADC采样数据处理也是使用离散FFT。离散FFT的输入点数和输出点数相同。假设我们使用1MHz采样率对一个信号进行采样，一共65536个采样点。那么1Mhz带宽内所有信号的幅值和频率信息被分配在这65536个点上，第32768个点表示频率为0.5Mhz的信号幅值。假设我们把采样率提高到2Mhz，还是采65536个点，也就是2Mhz带宽内所有信号的幅值和频率信息被分配在这65536个点上，变化是频谱图的bin点的频率间隔变大。因此，在采样率变大，采样点数不变的情况下，根据离散FFT所得的频谱图计算所得的噪声是减小。

其实要想减少噪声影响，还可以在ADC的输入端加一个低通滤波器，截至频率可以设置为2倍的信号带宽。在过采样的过程中，将用不到的带宽范围内的噪声滤除掉。

过采样的公式推导

我们在上面给出了信噪比SNR的换算公式，那么下面这个公式想必了解ADC动态性能参数的都接触过，其中N表示的是ADC的有效位。

实际上上式是在满足奈奎斯特采样定理的情况下得到的，即测试信号的带宽等于1/2采样率。实际上完整的ADC信噪比SNR的计算公式应该如下式。fs为采样率，BW为信号带宽。

根据上式可以得出，当采样率等于8倍信号带宽时信噪比SNR可以提升6.02dB。对应的有效位提高1个bit。

介绍完过采样的公式推导了是不是还有疑问，为什么在实际的过采样操作中时进行N次采样求平均呢。其实可以这样理解，假设我们用8倍信号带宽做过采样，采四次求平均，实际采样率变为2倍的信号带宽。等效于基于奈奎斯特定理采样一次。也就是说4次采样求平均为一次过采样的话，可以提高1位的分辨率。

需要注意的是，实际的过采样实现的过程中需要对采样数据加噪处理，并且如果单纯四次采样求平均的话是不会提高数据的分辨率的，为了提高数据的分辨率，需要将采样求和所得的数据进行抽取操作。最常用的数据抽取操作就是对求和数据右移N位，N表示的是过采样次数。

过采样不仅是理论上的优化手段，更是工程实践中突破ADC性能瓶颈的关键。掌握它，意味着你能在设计中实现更高精度、更强鲁棒性。现在，是时候把它应用到你的项目中了。