EEPW论坛

各位工程师朋友们，你是否曾遇到这样的困扰：精心设计的采集系统，ADC测量精度却总是不达标？明明选择了高分辨率ADC，实测结果还是差强人意？

别着急！本期我们带你彻底搞懂精度问题，掌握软硬结合的解决方案！

01两个关键概念

在提升精度前，先来介绍两个容易混淆的词：

准确度vs 精确度

准确度（accuracy）：测试值与理论值的偏差，偏差越大准确度越低

精确度（precision）：每次测试值之间的偏差，偏差越大精确度越低

根据准确度和精确度可以分为以下四种：

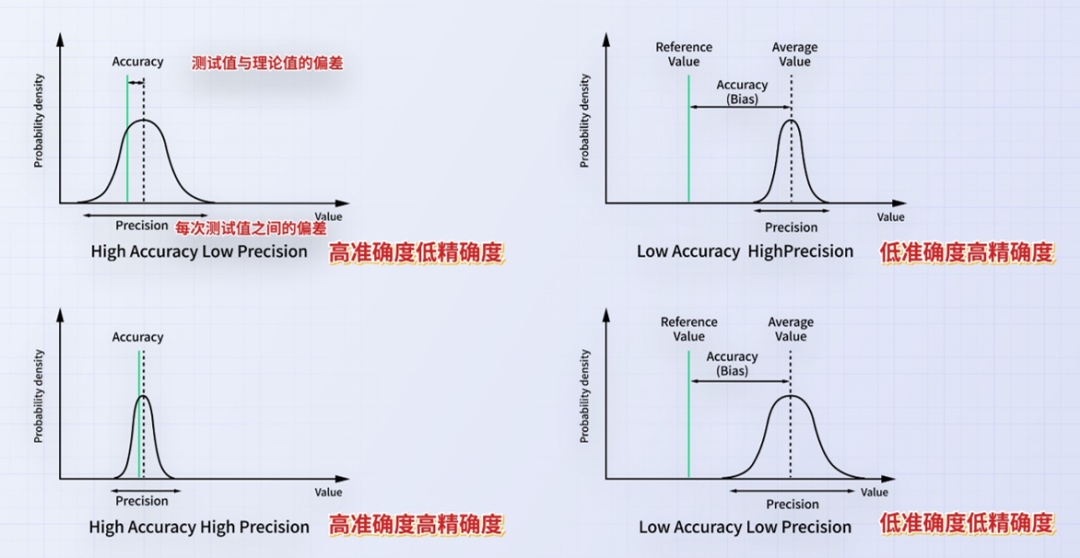
图1：四种偏差情况

准确度的高低根据测试数据的平均值与理论值的偏差来确定，精确度的高低根据测试数据的标准偏差来确定。

在使用ADC中往往遇到的是Low Accuracy, High Precision（低准确度，高精确度）。

电路板的功能越来越丰富，器件越来越多，有传感器（感知信号，将信号转换为电流或电压），运放（对信号进行缓冲，滤波，放大，电流-电压转换）， ADC（实现模拟数字转换），FPGA 或者 MCU等数字芯片，设计好每一个器件都是件富有挑战的事。

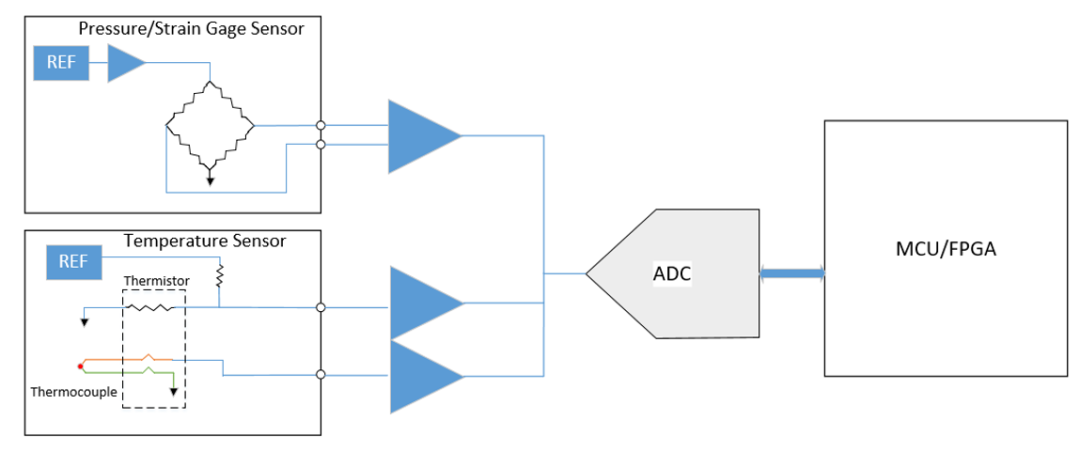
图2：电路板器件示意图

02误差从哪里来？

即使在PCB布局合理， 电源供电稳定，ADC基准设计合理的情况下，实际测试的值与理论值也会存在偏差。这些偏差是怎么产生的呢？ 运放自身的偏置电压、运放的偏置电流流过电阻产生的偏置电压、运放的失调电流、电阻的精度、ADC的offset误差、ADC的增益误差等，这些都会引起ADC转换结果与实际传感器输出值有偏差。

这些误差按起因大致可以分为：失调误差， 增益误差， 非线性误差、噪声误差。

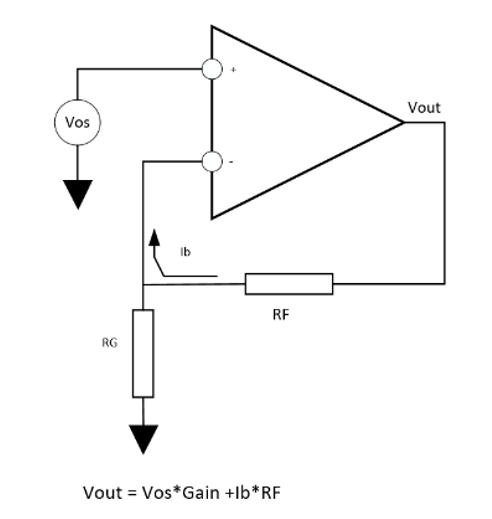
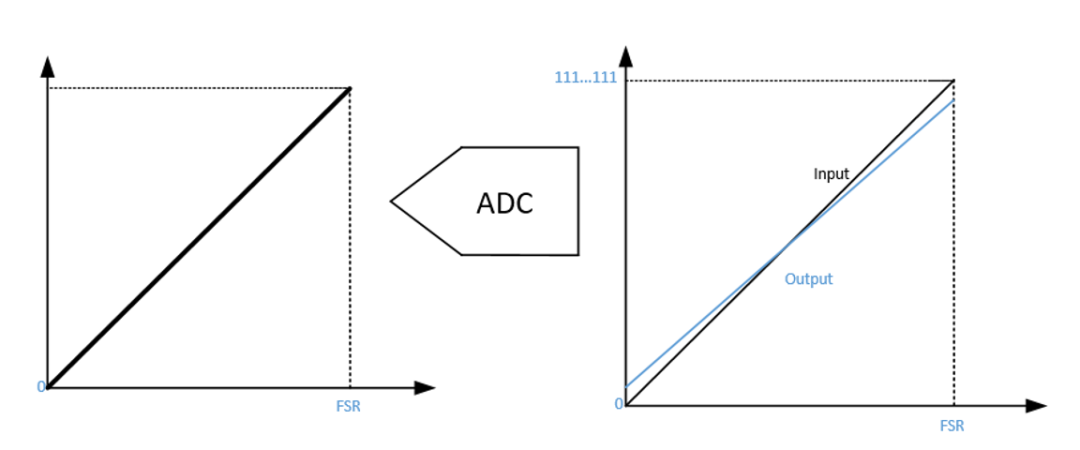
图3：误差来源

失调误差（Offset Error）：反映的是理论过零点与实际过零点的偏差，有正失调误差和负失调误差之分。正失调误差： 输出0到1（或1到2）跳变点的输入电压小于理论跳变点电压，理论电压与实际跳变电压的差值即为正失调误差。负失调误差： 输出0到1跳变点的输入电压大于理论跳变点电压，理论电压与实际跳变电压的差值即为负失调误差。

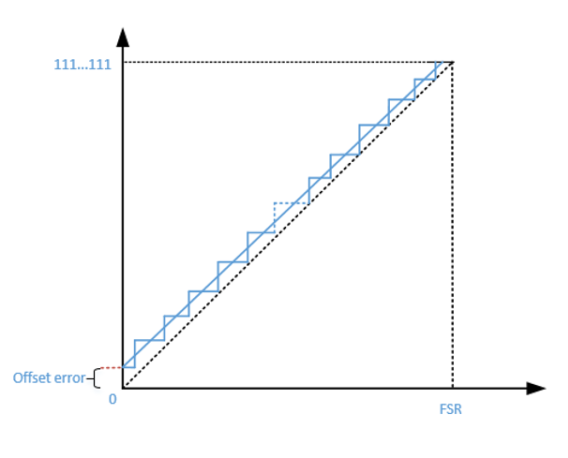
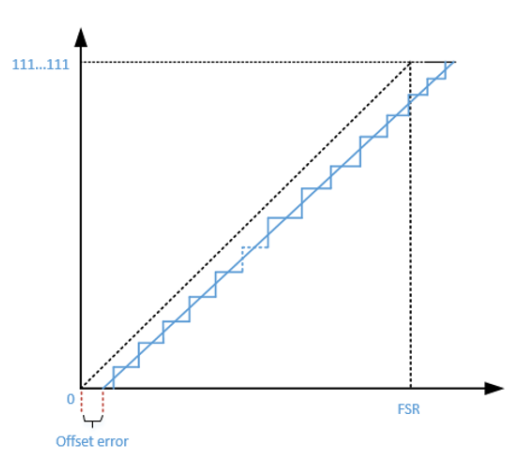
图4：失调误差

增益误差：理想传输函数与实际传输函数的偏差。在消除失调误差的影响后，系统第一次饱和输出时，实际输入与理论输入的偏差，或者实际输出与理论输出的偏差。

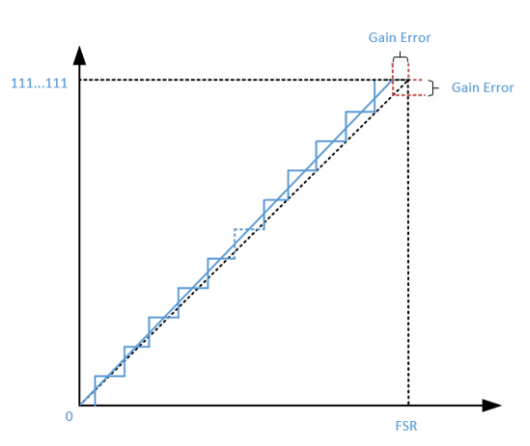
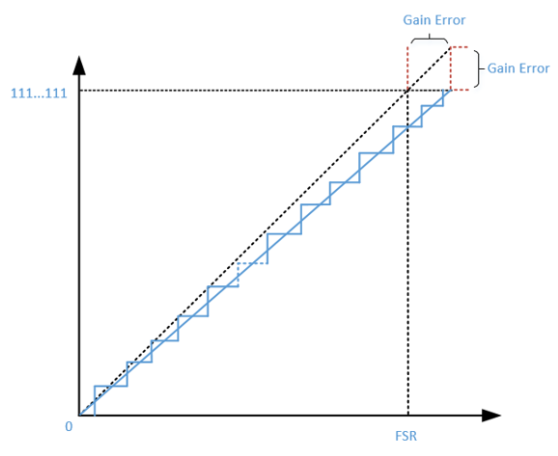
图5：增益误差

实际测试中，测试的满量程（FSR Full Scale Range）误差包含offset error，真正的增益误差Gain error需要去除offset error。

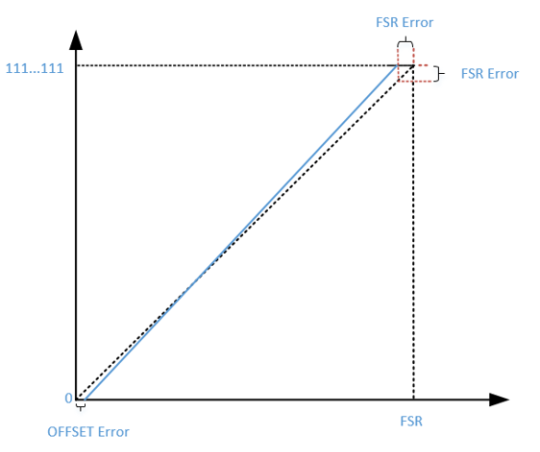
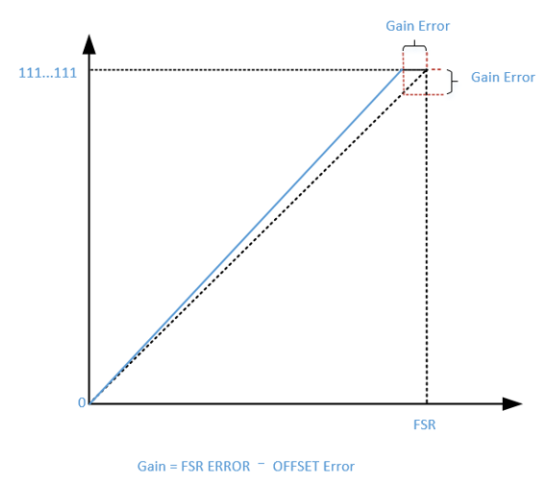
图6：实际测试中的误差

03实用校准方案

针对失调误差和增益误差可以使用两点法校准和分段法校准。如果线性度较好，选择两点校准，线性度较差情况下推荐使用分阶段校准，这里介绍如何使用两点进行校准。

选择两个测试点：VIN1, VIN2

记录VIN1和 VIN2 输入时的系统输出 VOUT1 , VOUT2

计算斜率：Slope_m = (VOUT2-VOUT1)/(VIN2-VIN1),

计算失调：Offset_m = VOUT2-VIN2*Slope_m

校准值：Vin_cal = (VOUT - Offset_m ) / Slope_m

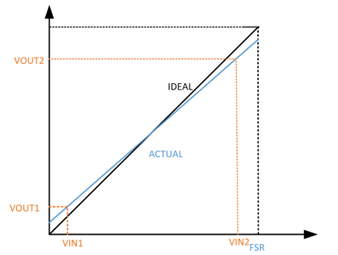
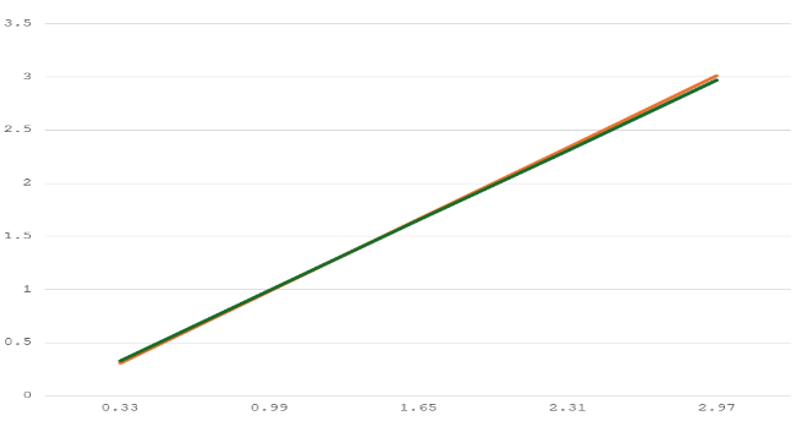
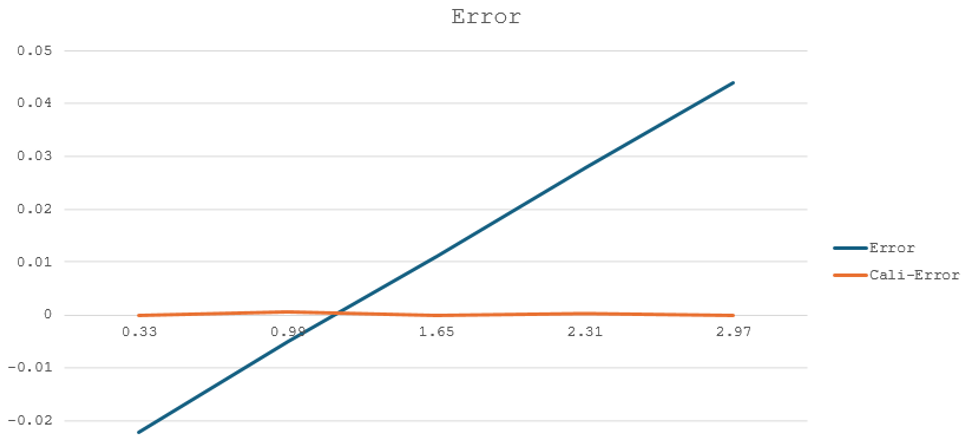
图7：校准方法

04噪声误差如何处理？

噪声引起的误差在满足奈奎斯特采样率的要求前提下，可以用平均等滤波算法通过牺牲采样率来提高，即Sigma Delta ADC的核心原理。

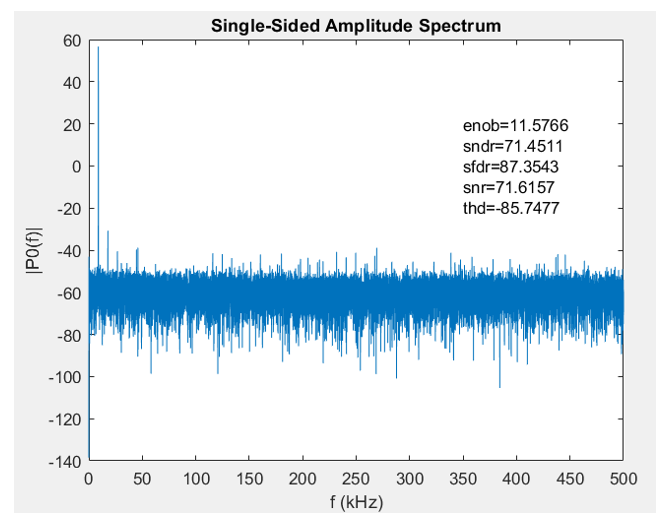
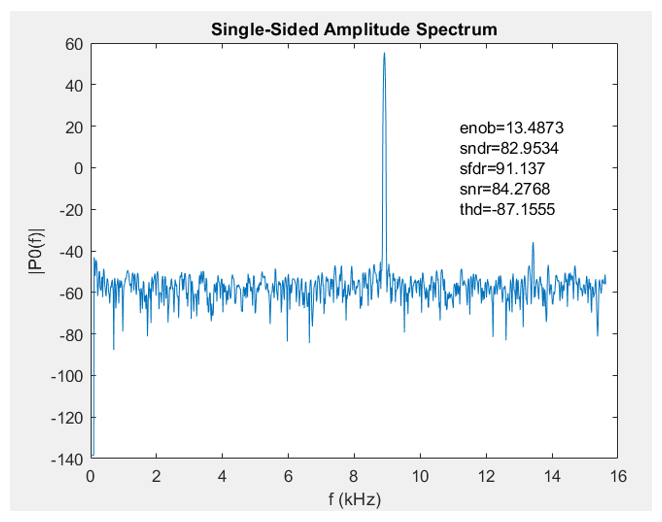
图8：噪声滤波

上面介绍了由offset error和gain error引起的系统误差，可以通过两点校准算法来实现，噪声引起的误差通过数字滤波算法来降低（会在下一集ADC小课堂中展开讲解）。

所以我们在设计高精度采集系统时，要软硬结合，即选择性价比高的芯片同时加上软件的优化来满足设计需求。