在过程控制中,按偏差的比例(P)、积分(I)和微分(D)进行控制的PID控制器(亦称PID调节器)是应用最为广泛的一种自动控制器。它具有原理简单,易于实现,适用面广,控制参数相互独立,参数的选定比较简单等优点;而且在理论上可以证明,对于过程控制的典型对象──“一阶滞后+纯滞后”与“二阶滞后+纯滞后”的控制对象,PID控制器是一种最优控制。PID调节规律是连续系统动态品质校正的一种有效方法,它的参数整定方式简便,结构改变灵活(PI、PD、…)。
PID增量式算法
离散化公式:
注:各符号含义如下
u(t);;;;; 控制器的输出值。
e(t);;;;; 控制器输入与设定值之间的误差。
Kp;;;;;;; 比例系数。
Ti;;;;;;; 积分时间常数。
Td;;;;;;; 微分时间常数。
T;;;;;;;; 调节周期。
对于增量式算法,可以选择的功能有:
(1) 滤波的选择
可以对输入加一个前置滤波器,使得进入控制算法的给定值不突变,而是有一定惯性延迟的缓变量。
(2) 系统的动态过程加速
在增量式算法中,比例项与积分项的符号有以下关系:如果被控量继续偏离给定值,则这两项符号相同,而当被控量向给定值方向变化时,则这两项的符号相反。
由于这一性质,当被控量接近给定值的时候,反号的比例作用阻碍了积分作用,因而避免了积分超调以及随之带来的振荡,这显然是有利于控制的。但如果被控量远未接近给定值,仅刚开始向给定值变化时,由于比例和积分反向,将会减慢控制过程。
为了加快开始的动态过程,我们可以设定一个偏差范围v,当偏差|e(t)| β时,即被控量接近给定值时,就按正常规律调节,而当|e(t)|>= β时,则不管比例作用为正或为负,都使它向有利于接近给定值的方向调整,即取其值为|e(t)-e(t-1)|,其符号与积分项一致。利用这样的算法,可以加快控制的动态过程。
(3) PID增量算法的饱和作用及其抑制
在PID增量算法中,由于执行元件本身是机械或物理的积分储存单元,如果给定值发生突变时,由算法的比例部分和微分部分计算出的控制增量可能比较大,如果该值超过了执行元件所允许的最大限度,那么实际上执行的控制增量将时受到限制时的值,多余的部分将丢失,将使系统的动态过程变长,因此,需要采取一定的措施改善这种情况。
纠正这种缺陷的方法是采用积累补偿法,当超出执行机构的执行能力时,将其多余部分积累起来,而一旦可能时,再补充执行。
数字PID控制算法
首先,将连续的系统离散化。
计算机控制是一种采样控制,它只能根据采样时刻的偏差值计算控制量,因此,连续PID控制算法不能直接使用,需要采用离散化的方法。在计算机PID控制中,使用的是数字PID控制器。
采样周期T为1ms,采用Z变换对G(S)进行离散化,离散化后的被控对象为:
Transfer function:
0.06684 z^2 - 0.1322 z + 0.06538
z^3 - 2.222 z^2 + 1.445 z - 0.2229
可得系统的差分方程:
y(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*u_1+num(3)*u_2+num(4)*u_3;
num =[0 0.0668 -0.1322 0.0654]
den =[1.0000 -2.2219 1.4448 -0.2229]
在输入信号为单位阶跃信号时,运行附录2的数字PID程序,可得系统的响应如下:
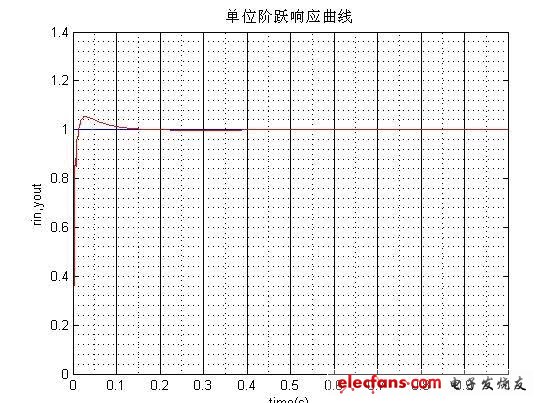
在PID参数:kp=10;ki=3000;kd=0; 调节时间0.15s0.2s; 无稳态误差, 超调量4%>2%。其中超调量过大不满足系统的设计要求。
利用Matlab /Simulink软件,构建了电机控制系统的速度仿真模型。通过仿真结果可以看出系统能平稳运行,具有较好的静、动态特性。在此仿真模型基础上,可以十分便捷地实现进行参数选择、调整及仿真。因此,可以从整体角度出发对伺服系统整体参数的优化和调整进行研究。也为实际伺服系统的设计和调试提供了新的思路

 我要赚赏金
我要赚赏金

