EEPW论坛

凡用二阶微分方程描述的电路，称为二阶电路。二阶电路中含有两个独立的储能元件。本节以串联电路为例，讨论二阶电路的零输入响应。

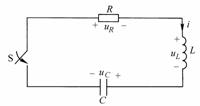
图8-7-1

图8-7-1为串联电路，当时，假设电容C曾充过电，初始电压为，电感L处于零初始状态，即。在时刻，开关S闭合，求零输入响应、与。

如图8-7-1所示选取各电压、电流的参考方向。开关S闭合后，根据基尔霍夫电压定律列写描述电路的微分方程：

（式8-7-1）

（式8-7-1）中有两个未知变量i和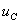。将代入上式消去，得到：

即：

（式8-7-2）

也可以得到：

（式8-8-3）

（式8-7-2）与（式8-7-3）形式完全一致，都是线性常系数二阶齐次微分方程，可任选其中一式求解，现选择（式8-7-2）。求解二阶微分方程，需要两个初始条件来确定积分常数。

根据换路定则：

，

特征方程为：

特征根为：

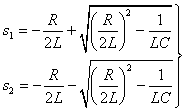（式8-7-4）

特征根只与电路结构和参数有关。

下面分三种情况讨论方程的解。

（1）当即时，过渡过程是非周期情况，也称为过阻尼情况。此时特征方程有两个不相等的负实根。通解的一般形式为：

（式8-7-5）

电流：

（式8-7-6）

其中积分常数A1、由初始条件确定，对（式8-7-5）（式8-7-6）取时刻值：

，

由初值：

，

联立求解上两式得：

（式8-7-7）

将A1、代入（式8-7-5）（式8-7-6）得：

电容电压：

（式8-7-8）

电流：

电感电压：

又因，于是：

（式8-7-9）

（式8-7-10）

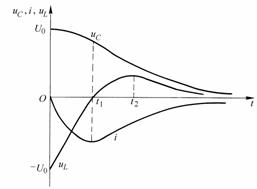
图8-7-2

、、随时间变化的曲线如图8-7-2所示。在（式8-7-8）中，包含两个分量，S1、S2都为负值，且，故比衰减得快，这两个单调下降的指数函数决定了电容电压的放电过程是非周期的。

电感电压在时初值为，在时，由于电流不断负向增加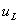，为负；在后，电流负向减少，为正，最终衰减至零。

如果，或，时，分析过程与上相同。

（2）当即时，过渡过程是临界阻尼情况，此时特征方程有两个相等的负实根。

（式8-7-11）

电容电压的一般形式为：

（式8-7-12）

电流：

（式8-7-13）

由初始条件确定积分常数、：

，

解之得：

，

因此：

（式8-7-14）， （式8-7-15） （式8-7-16）

、、随时间变化的曲线与图8-7-2所示的曲线相似，响应仍然是非周期性的，非振荡性的。

（3）当即时，过渡过程是欠阻尼情况，是周期性振荡情况。此时特征方程有两个实部为负的共轭复根。令，称为衰减系数，为谐振角频率，称为振荡角频率，则特征根为：

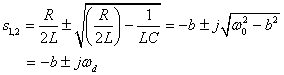（式8-7-17）

电容电压的一般形式为：

（式8-7-18）

电流：

（式8-7-19）

由初值确定积分常数A、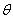，对（式8-7-18）、（式8-7-19）取时刻的值，得到：

联立求解得：

， （式8-7-20）

于是：

（式8-7-21）

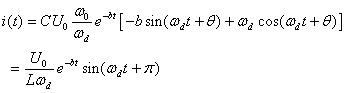（式8-7-22）

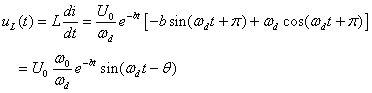（式8-7-23）

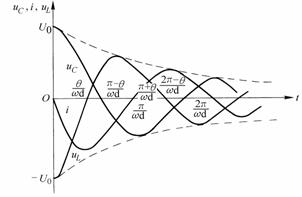
图8-7-3

、、的波形如图8-7-3所示，它们都是振幅按指数规律衰减的正弦波，图中虚线为包络线。当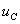达到极大值时，为零；当达到极大值时，I为零。这种幅值逐渐减小的振荡称为阻尼振荡或衰减振荡。衰减系数b越大，振幅衰减越快；b越小，振幅衰减越慢。阻尼振荡角频率决定于由路本身的参数，电阻减小，则衰减系数减小，衰减减慢，在的极限情况下，衰减系数，响应变成等幅振荡，也称为无阻尼振荡。无阻尼振荡角频率等于谐振角频率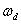，这时（式8-7-21）（式8-7-22）（式8-7-23）变为：

（式8-7-24）

（式8-7-25）

（式8-7-26）

上述无阻尼振荡不是由激励源强制作用所形成的，是零输入响应，因此称为自由振荡。下面从能量转换角度分析电路的久阻尼周期性振荡过程。

例8-7-1 如图8-7-4所示电路，当时开关S闭合。已知，，，。试分别计算、及时的。

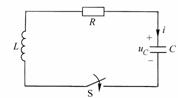
图8-7-4例8-7-1附图

解：图8-7-4所示是一个RLC串联电路，利用前面的分析结果求解。

（1）时，，过渡过程为过阻尼情况。

，

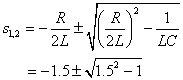
根据换路定则：

，

于是：

求得：

，

故：

（2）当时，，过渡过程为临界阻尼情况

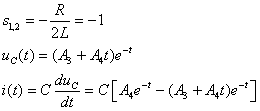
由初始条件得：

，

解得：

，故：

（3）当时，，过渡过程为欠阻尼情况：

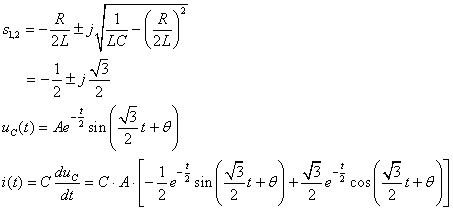
由初始条件得：

，

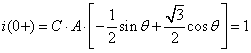
解得：

故：