EEPW论坛

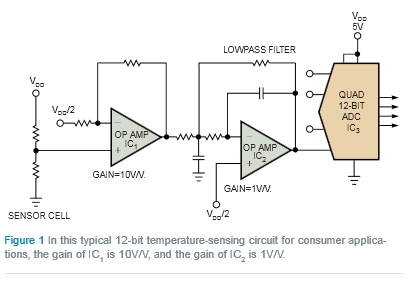
在您很难为消费类电路（如图 1 所示的温度传感器电路）选择器件时，只要为每个插槽选择绝对最佳性能的部件就可迅速解决这一问题。这种说法是真还是假？这种逻辑会让您深信：您的电路一开始就会正常工作。然而，当您试图在您所用产品的性价比因素之间进行权衡时，这种逻辑恐怕就不是万能的了。

在图 1 中，可以注意到信号链末端有一个 12 位转换器。那么，在 ADC 前面使用最高性能模拟产品是否适当？如何判定哪些产品对于您的系统来说足够好？您对“足够好”的定义可能是避免生产车间通告或现场故障。

您可以不选择最佳产品，而是采用 RSS（和的平方根）代数方法来解决。所依照的准则是将信号保持在 ADC 满量程动态范围内。影响动态范围的产品特性是系统累积失调及增益误差。

例如，假设 IC1 和 IC2 的最大失调误差是 0.5mV。ADC 的失调误差是 ± 1LSB 或 ±1.22 mV (ADC 的满量程范围是 5V)。传感器单元与 IC1 放大器的增益误差取决于 ±1% 的最大电阻器容差以及 ±2% 的最大传感器至电阻器容差。ADC 在满量程下分配的增益误差为 0.098% 或整好等于 4.9 mV 的最大值。

要确定电路的动态范围极限，如果将所有这些项目进行组合，您会计算出失调与增益的整合 RSS 值，将这些误差带到 ADC 的输入端。使用 RSS 方程式对几个统计上相互独立的项目进行平方和方根计算。不能将 RSS 方程式应用于具有相关变量（在统计上不独立）的实体。

例如，最差的传感器电阻失调误差为 ±94 mV×10V/V。放大器增益级 IC1 的分量为 ±500 µV×10，滤波器级 (IC2) 的失调误差是 ±500 µV，而 ADC(IC3) 的失调误差则为 ±1.22 mV。ADC 输入端的适当累积失调误差为 =940 mV。该计算表明传感器单元对误差的贡献最大，而且受放大器和 ADC 的影响极小。依照相同逻辑，还可使用 RSS 公式计算该电路中可限制四级动态范围的增益误差贡献。

因此，在进行第一次消费类产品选择时，您可使用 RSS 进行计算。这些计算可帮助您做出符合逻辑的低成本产品决策。采用这一步时，应确保在制造流程中使用相同的评估法，以便对这些器件所用工艺（例如焊接回流）的影响以及环境所带来的使用寿命终止影响进行定量。