EEPW论坛

Rm=Le/(u*A)(Le是磁环长度)  Rm是磁阻

L（电感）=N2/Rm (N的平方)

磁势

磁源提供磁力的的最大能力 根据安培环路定律有对磁场强度H沿长度元dl的积分等于线圈的匝数乘以积分曲线包围的电流的代数和，对一载有电流I、匝数为N的励磁线圈，穿过线圈回路的磁势NI。 2磁势说明编辑磁源对外开环时产生的能量形式为磁场，导磁体与磁源闭合形成的回路产生磁通，导磁体都有磁阻，此时如果把它的负载磁阻看做为零（即无漏磁损耗），此时磁源的最大磁通能力就是磁势

B为磁感应强度,S为面积，L为磁源长度，那么磁势等于B*S*L
磁动势，的标准定义是电流流过导体所产生磁通量的势力(force)[2]，是用来度量磁场或电磁场的一种量，类似于电场中的电动势或电压。它被描述为线圈所能产生磁通量的势力[2]，这样科学家就能够用它来衡量或预见通电线圈实际能够激发磁通量的势力[2]。此外，永久磁铁也会有磁动势 F=ΦRm（Φ=B*S S为截面积），Rm=L/μA F = NI F = HL(H为磁场强度，与磁密度B和磁路材料等有关） L表示磁路长度。 公式一：作用在磁路上的磁动势 F 等于磁路内的磁通量 Φ 与磁阻Rm的乘积。 公式二：通电线圈产生的磁动势 F 等于线圈的匝数 N 和线圈中所通过的电流 I 的乘积，也叫磁通势，磁动势F的单位是安培(A)。 公式三：F 是磁场强度H在磁路L上的积分。 磁动势的标准定义是电流流过导体所产生磁通量的势力(force)，是用来度量磁场或电磁场的一种量，类似于电场中的电动势或电压。它被描述为线圈所能产生磁通量的势力，这样科学家就能够用它来衡量或预见通电线圈实际能够激发磁通量的势力。此外，永磁材料也以某种方式表现出磁动势。 感应电机的磁动势为:N-绕组匝数，单位为次数(turns)

• I-绕组中的电流，单位为安培 (A)
• -磁通量，单位为韦伯 (Wb)
• -磁路的磁阻，单位为安培/韦伯 (A/Wb)

后者又被称为霍普金斯定律或磁路欧姆定律. 单安培-匝数(At), 国际单位制。代表一匝导线线圈流过1安培电流时所产生的磁势。 吉伯 (gilbert 或Gi),是IEC1930 [1]提出的单位。属于厘米-克-秒制中的磁动势单位。与安培-匝数定义不同，是一个比安培-匝数稍小的单位。这个单位是以英国物理学家和哲学家威廉·吉尔伯特 (1544–1603)的名字命名的。
磁位差
magnetic difference of potential
    恒定磁场中无传导电流分布的空间区域内两点a与b之间的标量磁位之差（又称磁位降）。记为U m。它与静电场中的电位差相似。其定义为
   式中H为沿ab曲线长度元dl处的磁场强度。
   在国际单位制(SI)中，磁位差的单位为安(A)。
磁位差
magnetic difference of potential
    恒定磁场中无传导电流分布的空间区域内两点a与b之间的标量磁位之差（又称磁位降）。记为U m。它与静电场中的电位差相似。其定义为
   式中H为沿ab曲线长度元dl处的磁场强度。
   在国际单位制(SI)中，磁位差的单位为安(A)。 磁通势 magnetomotive force
    磁路中的一个物理量，相当于电路中的电动势。环绕一闭合回路l的磁通势Fm等于该回路的磁场强度H与此回路长度元dl矢量的点积沿l的积分，即
   式中β为dl与其处的H的夹角。按安培环路定律，沿一闭合回路的磁通势等于穿过该回路所限定的面上的电流 ΣI 即
   对一载有电流I、匝数为W的励磁线圈，穿过线圈回路的磁通势Fm＝WI。
   在国际单位制（SI）中，磁通势的单位为安（A）或安匝
磁阻Rm=L/uS，对于一般导磁材料而言，u不是常数，u与磁场强度H有关，即磁阻还与磁动势NI（或磁压降HL）相关，不同的磁动势NI或磁压降HL下，磁阻Rm不同。在定量计算时，不能用一个固定的参数表示磁阻。
磁路计算基础

      直接应用Maxwell电磁场方程组，根据给定的边界条件求解磁场的分布规律一般是很困难的，即使利用大型计算机求其数值解，工作量和费用仍然十分可观，所以工程上大量的问题还是简化为磁路来加以计算。

      凡是磁通或磁力线所经过的闭合回路就叫磁路。每个磁通管都可以看成一条磁路，整个磁场就是由这许许多多的磁路并联而成的。一般情况下磁力线漫步在整个空间，不容易找到一条磁通比较集中通过的磁路，因此计算就比较麻烦。

      在电磁机构中，为了获得较大的磁通，通常采用铁磁材料制作零件，使磁通主要集中在导磁材料中，这样就形成一个确定的磁路，使计算简化了。计算所用到的一些概念和定律，如磁势、磁通、磁阻、磁位差、磁路的欧姆定律和基尔霍夫（Kirchhoff）二定律等，都是直接从磁场的概念和定律转化而得来的，但是在形式上与电路非常相似。下面简要介绍磁路计算中的几个基本概念。

      1、磁势、磁通、磁阻和磁压降
      图2-2所示为最简单磁系统的磁路和电路的对比。该磁系统只有一个圆环状铁心，圆环状铁心上绕有W匝线圈。当线圈通以电流I后，绝大部分磁力线都会集中在磁导率很高的铁心中（若线圈均匀而又紧密地绕在整个圆周上，则磁通实际上几乎全部局限在环内)。

      若圆环的内、外径之差远比平均直径小，则可以认为磁通在横截面积S上的分布是均匀的，因此铁心各处的B（或H)可以认为相等。沿圆环平均周长lp应用安培环路定律，并注意到各处的H和dl同方向，即cosθ=1，因此得

      考虑到H=B/μ（μ为铁心材料的磁导率)，可得到

      代入上式则得

式中，ρ0为磁导率μ的倒数，称为“磁阻系数”，即

      我们将线圈电流I与匝数W的乘积IW称为“磁动势”，简称“磁势”，并将磁势与磁通Φ之比定义为磁阻R，即

      则对于均匀磁场，由式（2-82)可得

      因此，磁路中磁通与磁势和磁阻的关系可以表示为

      这个关系式就称为磁路的欧姆定律。注意，它和电路中的全电路欧姆定律在形式上很相似，如图22b所示，即电路中的电流I与电动势E成正比例而和电路中的电阻R（含电源内电阻)成反比，即I=E/R。

      磁势的单位为安，但习惯上往往称它为安匝，以便和电流相区别，因为匝数本身并没有单位，它只是表示线圈电流作用的倍数而已。

      在磁路计算中，我们比较习惯于应用磁导Gc，磁导就是磁阻的倒数，即

      磁导的单位，在制中为（H)或（Wb/A)，而在制中为（Mx/A)。
      在电路中，电阻两端的电位差U称为电阻压降，简称“电压降”，可表示为

      同样，在磁路中，磁阻两端的磁位差U称为“磁压降”，也表示为

      因为由式（2-80)得

      磁路中，磁场强度H具有另一种含义，即由式（2-88)得H=ΦR/lp（A/m)，因此，可以将H看成为磁路单位长度上的磁压降。

      必须指出，磁路和电路计算上的相似，绝不意味着两者的物理本质是一样的。从本质上说，在电动势的作用下，导线内确有电荷在流动。因此，当电流流过电阻时，电能就会转换为热能，使电阻发热。但在磁路中，磁通（或磁现象)是伴随着磁势（或电流)而建立的，也可以说，磁场就是电流的一种表现形式，在导磁体内并没有什么东西真在流动。所以，维持一个恒定不变的磁通并不需要消耗任何能量（当然，维持线圈电流还是需要从电源中吸取能量的，但是这个能量是消耗在线圈电阻中的)。

      2、等值磁路图
      因为磁路和电路在计算上有其相似之处，所以，在分析和计算某一磁系统时，常常模仿电路的表示形式将它表示成等值磁路图，等值磁路图中引用电路中代表电动势和电阻的符号来代表磁动势和磁阻。举一实例说明如下：

      图2-3a所示为拍合式磁系统。该系统的导磁磁路由插入线圈的铁心、L形的铁轭和能绕轴转动的吸片（也称衔铁)组成。线圈通电后，绝大部分磁通将通过铁心、铁轭、吸片以及吸片与铁心端面间的气隙δ1（称为主工作气隙)而构成闭合磁路，而这些磁通会对吸片产生吸力，因而称为主磁通Φδ。主磁通的平均磁力线如图中虚线所示。该磁系统的等值磁路图如图2-3b所示。

      注意：在绘制以上等值磁路图时只考虑了主磁通所经过的路径，所以是只有一个回路的简单磁路，其中本来是分布在整个铁心长度上的线圈磁势就可以用一个集中的磁势IW来表示。实际的情况是磁系统内还会有漏磁通存在，因此这样的等值磁路图是近似的。

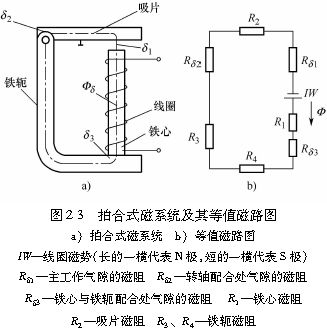
      图2-4a所示为E形拍合式磁系统，其等值磁路图如图2-4b所示。将具有两个及两个以上回路（或网孔)的磁路称为“复杂磁路”。

      3、磁路基尔霍夫二定律
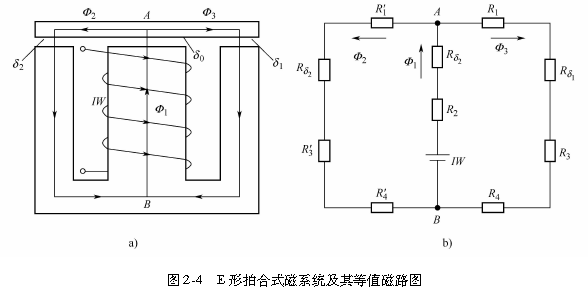
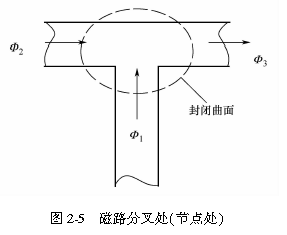
      计算具有分支的多回路电路时须运用电路的基尔霍夫二定律，同样在计算复杂磁路时，也可以运用类似的磁路基尔霍夫二定律。磁路基尔霍夫二定律实质上就是磁通连续性原理和安培环路定律在磁路中的应用。与电路相似，我们把同一磁通通过的路径称为“支路”，而把三条或三条以上的支路会聚处称为“节点”。

      磁通连续性原理指出磁场中穿出（或穿入)一个封闭曲面的磁通总和恒为零。如果我们把封闭曲面取在磁路的节点处，如图2-5所示，显然应有

      即汇聚在任一节点上的磁通的代数和恒等于零，这就是磁路的基尔霍夫第一定律。高斯定理规定：进入节点的磁通取负值，而离开节点的磁通取正值。因此，对于图2-5应有

      同样，根据安培环路定律也可以得到相应的磁路基尔霍夫第二定律，即对于任一闭合磁路，沿某一环绕方向，其磁压降的代数和恒等于该回路中磁势的代数和，即

      如果磁路各分段的B（或H)可假定为常数，并且其方向与环路方向一致，则磁路基尔霍夫第二定律也可以表示为

      式（2-92)和式（2-93)可以视计算方便选用，其中磁压降的表示方法也可以混合使用。在使用中应注意决定各项正、负的规则：先规定各支路中磁通的正方向，如果Φ（或H)的正方向与环绕方向一致时，则该段的磁压降为正值，反之则为负值；若磁动势的正方向和环绕方向一致时，则该段的磁势为正值，反之为负值（磁动势正方向和线圈中电流正方向符合右手定则)。

      磁路基尔霍夫二定律对于任何形式的磁路都是普遍适用的，也就是说，不论导磁体的磁阻是线性的（即μ为常数)还是非线性的（即μ不是常数)，也不论是否考虑漏磁现象，磁路基尔霍夫二定律都是适用的。但是，如果我们假定铁磁阻为线性（即磁阻为常数)，那么只要绘出等值磁路图就完全可以应用计算电路的各种方法（如电阻的串并联计算法、支路电流法、回路电流法、叠加原理和等效发电机原理等)来解决磁路问题了。

      4、气隙磁导计算
      各种磁系统中都不可避免地存在气隙，包括工作气隙和非工作气隙。尽管气隙并不大，但由于空气的磁导率远远小于铁磁性材料的磁导率，气隙的磁阻仍然较大，工作气隙上的磁压降往往占去整个线圈磁势的绝大部分。因此，气隙磁导（磁阻)计算的准确与否，将严重地影响到整个磁系统的计算精度。下面将会看到气隙磁导对吸力计算的准确与否也是至关重要的。

      气隙磁导是气隙两端磁极间的磁压降Uδ与通过该气隙的磁通Φδ之比，即

      从上式中可以看出气隙磁导是气隙磁阻的倒数，即

      需要强调的是：根据上述磁导的定义，两磁极表面都必须是等磁位面，而Uδ是这两个等磁位面之间的磁位差。然而通常只有具有磁极但磁极不饱和时，其表面才能看作是等磁位面。

      我们知道

式中,S为磁极的表面积；δ为磁极间气隙。

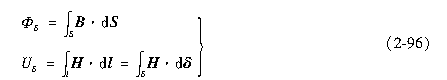
2.5.2永磁磁路的计算方法

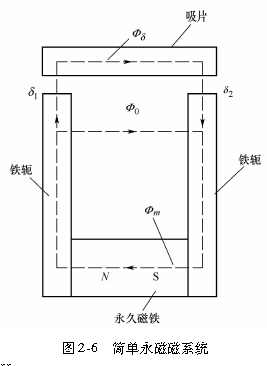
      在永磁磁路中，永久磁铁相当于一个磁势的作用，同时它又具有磁阻。计算时，磁路的基尔霍夫二定律仍然普遍适用，但是，要用永磁材料的退磁曲线来进行计算。和一般磁路计算一样，在计算永磁磁路时也有正、反两类任务，即已知工作气隙的磁通值，要求选择永久磁铁的材料并确定其尺寸;或者反之，已知各部分的材料和尺寸，要求计算工作气隙内的磁通值。分析永久磁铁工作点在退磁曲线上时的工作特点及其设计，如图2-6所示。

      磁路基尔霍夫第二定律可以证明，永久磁铁工作点Ba和Ha必须满足下列关系式，即

式中Gδ——工作气隙δ1和δ2的串联磁导，单位为H；
l——磁铁长度，单位为m；
S——磁铁横截面积单位为㎡;
σ——磁系统的漏磁系数，即其中Φm和Φσ分别为磁铁和工作气隙内的磁通值；
K∑——考虑磁路内非工作气隙和导磁体磁阻上的磁压降的一个系数，即

式中Uσ——工作气隙上的磁压降；
       Uc——非工作气隙和导磁体磁阻上的磁压降。
一般,K∑=1.2～1.4。
------------------------------------------------------------------------------------------- 磁阻Rm=L/uS，对于一般导磁材料而言，u不是常数，u与磁场强度H有关，即磁阻还与磁动势NI（或磁压降HL）相关，不同的磁动势NI或磁压降HL下，磁阻Rm不同。在定量计算时，不能用一个固定的参数表示磁阻。