EEPW论坛

OpenCV-Python系列之拉普拉斯算子

我们在上一个教程中前面的例子学习了使用Sobel边缘检测。原理是利用边缘区域像素值的跳变。通过求一阶导数，可以使边缘值最大化。如下图所示：

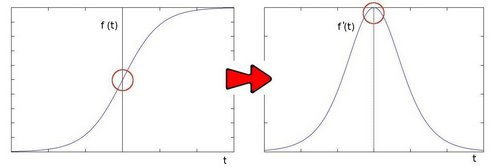
那么，如果求二阶导数会得到什么呢?

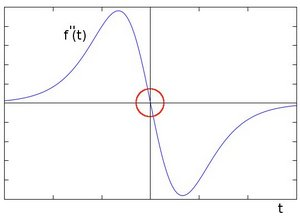
可以观察到二阶导数为0的地方。因此，可以利用该方法获取图像中的边缘。然而，需要注意的是二级导数为0的不只出现在边缘地方，还可能是一些无意义的位置，根据需要通过滤波处理该情况。

二阶微分

现在我们来讨论二阶微分，它是拉普拉斯算子的基础，与微积分中定义的微分略有不同，数字图像中处理的是离散的值，因此对于一维函数的一阶微分的基本定义是差值：

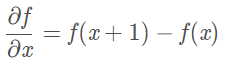
类似的，二阶微分定义为：

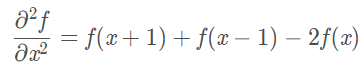
将一维函数扩展到二维：

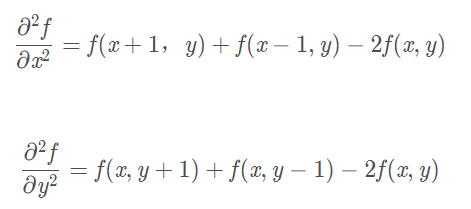
二阶微分的定义保证了以下几点：

1、在恒定灰度区域的微分值为0

2、在灰度台阶或斜坡的起点处微分值非零

可以看出，二阶微分可以检测出图像的边缘、增强细节

拉普拉斯算子

从上面的解释，可以看出二阶导数可以拥有边缘检测。由于图像是二维的，因此需要分别获取两个方向的导数。这里使用的是拉普拉斯算子来进行近似。

拉普拉斯算子用下面公式定义：

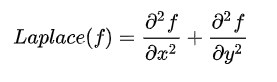
其中：

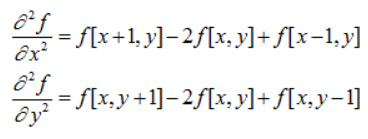
可以用多种方式将其表示为数字形式。对于一个3*3的区域，一般情况下被推荐最多的形式是：

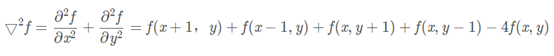
实现上式的滤波器模板为：

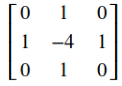
我们可以发现，拉普拉斯算子不需要向Sobel算子那样分别对x，y方向进行处理，它可以直接处理，现在我们来看看OpenCV中的拉普拉斯算子的函数原型：

dst = cv2.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])

如果看了上一个教程中对于Sobel算子的介绍，这里的参数应该不难理解。

前两个是必须的参数：

第一个参数是需要处理的图像；

第二个参数是图像的深度，-1表示采用的是与原图像相同的深度。目标图像的深度必须大于等于原图像的深度；

其后是可选的参数：

dst不用解释了；

ksize是算子的大小，必须为1、3、5、7。默认为1。

scale是缩放导数的比例常数，默认情况下没有伸缩系数；

delta是一个可选的增量，将会加到最终的dst中，同样，默认情况下没有额外的值加到dst中；

borderType是判断图像边界的模式。这个参数默认值为cv2.BORDER_DEFAULT。

我们来看代码：

import cv2
import numpy as np

img = cv2.imread("pie.png")
dst = cv2.Laplacian(img,cv2.CV_16S,ksize=3)
dst = cv2.convertScaleAbs(dst)
cv2.imshow("img",img)
cv2.imshow("res",dst)

cv2.waitKey(0)
cv2.destroyAllWindows()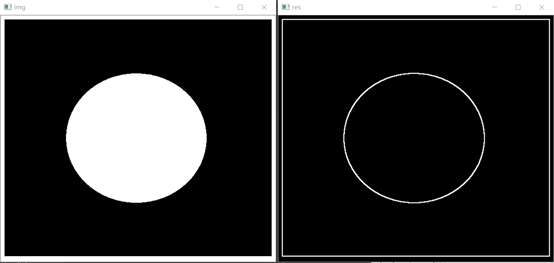

现在可以拿这个结果对比上一个教程的结果了，我们发现，这个结果要比上一个教程的结果好的多，对于边缘检测没有大的偏差。

然而事实上，这只是对于简单的图像而言，而对于一幅复杂的图像，那么边缘提取就有点爱莫能助了，我们来看代码：

import cv2
import numpy as np

img = cv2.imread("cat.jpg")
dst = cv2.Laplacian(img,cv2.CV_16S,ksize=3)
dst = cv2.convertScaleAbs(dst)
cv2.imshow("img",img)
cv2.imshow("res",dst)

cv2.waitKey(0)
cv2.destroyAllWindows()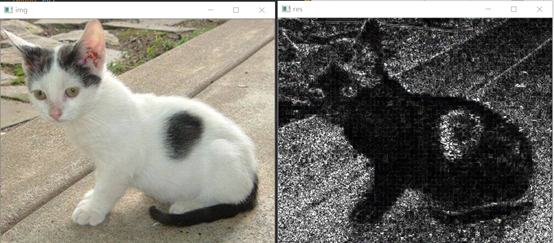

可以看到，对于较为复杂的图像，拉普拉斯算子的效果也并不是很好，由于二阶微分一定的局限性，目前的边缘检测还不够完美，我们需要一种综合的算法，而这将在下一个教程中介绍到。