EEPW论坛

OpenCV-Python系列之SURF算法

我们在上个教程讨论了SIFT算法用于检测特征点，SIFT算法对旋转、尺度缩放、亮度变化等保持不变性，对视角变换、仿射变化、噪声也保持一定程度的稳定性，是一种非常优秀的局部特征描述算法。但是其实时性相对不高。SURF(Speeded Up Robust Features)算法改进了特征了提取和描述方式，用一种更为高效的方式完成特征点的提取和描述。

SURF算法原理

SURF特征检测的步骤

1.        尺度空间的极值检测：搜索所有尺度空间上的图像，通过Hessian来识别潜在的对尺度和选择不变的兴趣点。

2.        特征点过滤并进行精确定位。

3.        特征方向赋值：统计特征点圆形邻域内的Harr小波特征。即在60度扇形内，每次将60度扇形区域旋转0.2弧度进行统计，将值最大的那个扇形的方向作为该特征点的主方向。

4.        特征点描述：沿着特征点主方向周围的邻域内，取4×4个矩形小区域，统计每个小区域的Haar特征，然后每个区域得到一个4维的特征向量。一个特征点共有64维的特征向量作为SURF特征的描述子。

构建Hessian

构建Hessian矩阵的目的是为了生成图像稳定的边缘点(突变点)，跟Canny、拉普拉斯边缘检测的作用类似，为特征提取做准备。构建Hessian矩阵的过程对应着SIFT算法中的DoG过程。

黑塞矩阵(Hessian Matrix)是由一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。由德国数学家Ludwin Otto Hessian于19世纪提出。

对于一个图像I(x,y)，其Hessian矩阵如下：

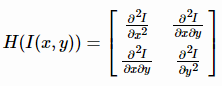
H矩阵的判别式是：

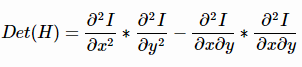
在构建Hessian矩阵前需要对图像进行高斯滤波，经过滤波后的Hessian矩阵表达式为：

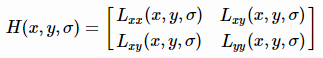
其中(x,y)为像素位置, L(x,y,σ)=G(σ)∗I(x,y),代表着图像的高斯尺度空间，是由图像和不同的高斯卷积得到。

我们知道在离散数学图像中，一阶导数是相邻像素的灰度差：

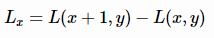
二阶导数是对一阶导数的再次求导：

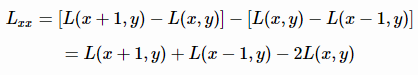
反过来看Hessian矩阵的判别式，其实就是当前点对水平方向二阶偏导数乘以垂直方向二阶偏导数再减去当前水平、垂直二阶偏导的二次方：

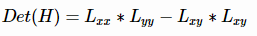
通过这种方法可以为图像中每个像素计算出其H行列式的决定值，并用这个值来判别图像局部特征点。Hession矩阵判别式中的L(x,y)是原始图像的高斯卷积，由于高斯核服从正太分布，从中心点往外，系数越来越小，为了提高运算速度，SURF算法使用了盒式滤波器来替代高斯滤波器L，所以在Lxy上乘了一个加权系数0.9，目的是为了平衡因使用盒式滤波器近似所带来的误差，则H矩阵判别式可表示为：

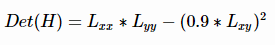
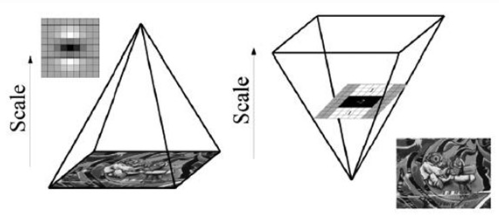
盒式滤波器和高斯滤波器的示意图如下：

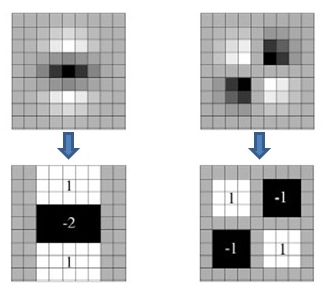
上面两幅图是9×9高斯滤波器模板分别在图像垂直方向上二阶导数Lyy和Lxy对应的值，下边两幅图是使用盒式滤波器对其近似，灰色部分的像素值为0，黑色为-2，白色为1。

那么为什么盒式滤波器可以提高运算速度呢？这就涉及到积分图的使用，盒式滤波器对图像的滤波转化成计算图像上不同区域间像素的加减运算问题，这正是积分图的强项，只需要简单积分查找积分图就可以完成。

构造尺度空间

同SIFT算法一样，SURF算法的尺度空间由O组S层组成，不同的是,SIFT算法下一组图像的长宽均是上一组的一半，同一组不同层图像之间尺寸一样，但是所使用的尺度空间因子(高斯模糊系数σ)逐渐增大；而在SURF算法中，不同组间图像的尺寸都是一致的，不同的是不同组间使用的盒式滤波器的模板尺寸逐渐增大，同一组不同层图像使用相同尺寸的滤波器，但是滤波器的尺度空间因子逐渐增大。如下图所示：

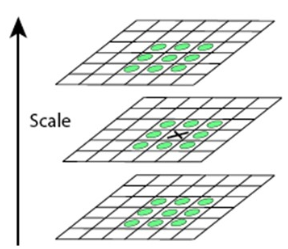
特征点过滤并进行精确定位

SURF特征点的定位过程和SIFT算法一致，将经过Hessian矩阵处理的每个像素点(即获得每个像素点Hessian矩阵的判别式值)与其图像域（相同大小的图像）和尺度域（相邻的尺度空间）的所有相邻点进行比较，当其大于（或者小于）所有相邻点时，该点就是极值点。如图所示，中间的检测点要和其所在图像的3×3邻域8个像素点，以及其相邻的上下两层3×3邻域18个像素点，共26个像素点进行比较。

初步定位出特征点后，再经过滤除能量比较弱的关键点以及错误定位的关键点，筛选出最终的稳定的特征点：

计算特征点主方向

SIFT算法特征点的主方向是采用在特征点邻域内统计其梯度直方图，横轴是梯度方向的角度，纵轴是梯度方向对应梯度幅值的累加，取直方图bin最大的以及超过最大80%的那些方向作为特征点的主方向。

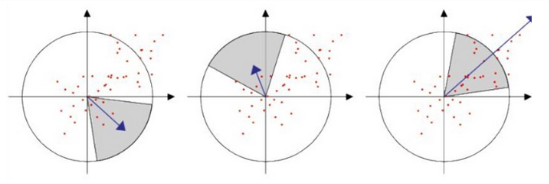
而在SURF算法中，采用的是统计特征点圆形邻域内的Harr小波特征，即在特征点的圆形邻域内，统计60度扇形内所有点的水平、垂直Harr小波特征总和，然后扇形以0.2弧度大小的间隔进行旋转并再次统计该区域内Harr小波特征值之后，最后将值最大的那个扇形的方向作为该特征点的主方向。该过程示意图如下：

生成特征描述

在SIFT算法中，为了保证特征矢量的旋转不变性，先以特征点为中心，在附近邻域内将坐标轴旋转θ（特征点的主方向）角度，然后提取特征点周围4×4个区域块，统计每小块内8个梯度方向，这样一个关键点就可以产生128维的SIFT特征向量。

SURF算法中，也是提取特征点周围4×4个矩形区域块，但是所取得矩形区域方向是沿着特征点的主方向，而不是像SIFT算法一样，经过旋转θθ角度。每个子区域统计25个像素点水平方向和垂直方向的Haar小波特征，这里的水平和垂直方向都是相对主方向而言的。该Harr小波特征为水平方向值之和、垂直方向值之和、水平方向值绝对值之和以及垂直方向绝对之和4个方向。该过程示意图如下：

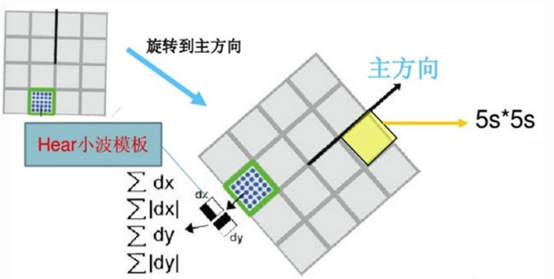
把这4个值作为每个子块区域的特征向量，所以一共有4×4×4=64维向量作为SURF特征的描述子，比SIFT特征的描述子减少了一半。

OpenCV中的SURF算法

跟SIFT一样，由于专利的原因，SURF目前也需要用低版本的OpenCV进行操作。

代码与SIFT的类似：

import numpy as np
import cv2
import matplotlib.pyplot as plt
 
img = cv2.imread('test32.jpg', 0)
 
surf = cv2.xfeatures2d.SURF_create(30000)
 
kp = surf.detect(img, None)
 
img2 = cv2.drawKeypoints(img, kp, None, (255, 0, 0), 4)
surf.setUpright(True)
surf.setHessianThreshold(40000)
kp = surf.detect(img, None)
img3 = cv2.drawKeypoints(img, kp, None, (255, 0, 0), 4)
 
plt.subplot(121), plt.imshow(img2),
plt.title('Dstination'), plt.axis('off')
plt.subplot(122), plt.imshow(img3),
plt.title('Dstination'), plt.axis('off')
plt.show()

结果如下：

目前我们也发现了，SIFT与SURF算法都受到了专利保护，在高版本的OpenCV中无法使用，我们在之后会介绍一些免费的算法。