EEPW论坛

本章将结合目前为止导出的公式，首先导出作为基础的降压模式的开关传递函数，使用状态平均化法，来导出在工作模式中未特殊化且被统一的传递函数。

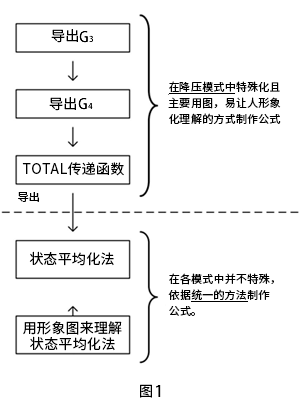
虽然之前已经简单的描述过，但我认为这是最难解且很难形象化示意的传递函数。因此，先将本章的描述流程总结在图1。

听到状态平均化法的话，总觉得可能会有很多人不了解。但是，使用此法的话，各转换器的传递函数就能根据统一的方法导出。这里我会尽可能用简单易懂的方式来描述，所以大家先挑战看看吧。

G3传递函数导出、频率特性

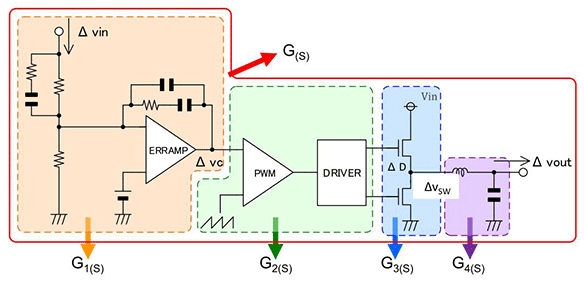
首先，我们有必要重温根据每个功能来对开关稳压器进行模块划分。在这里，先导出与开关模块的G3相关的传递函数。

首先，来计算出。请看图2。

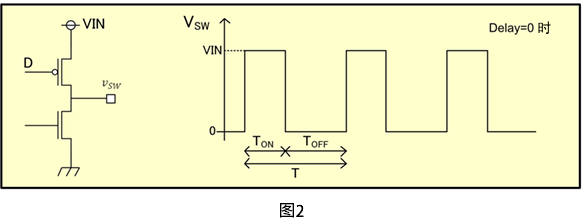
这就是降压模式的开关波形。VSW可用SW端子作为H(VIN)，L(O)的时间平均来描述，

因此，在公式4-1中，假设D→D+∆D、VSW→VSW+∆VSW的话，

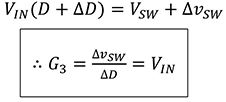
那么可导出。

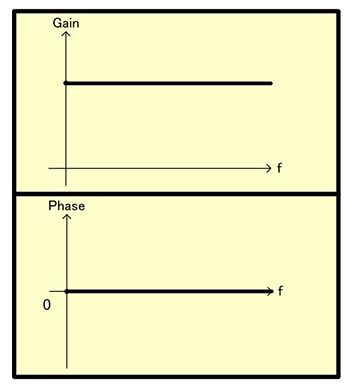
这个结果如右图所示，G3表示Gain一定相位不发生变化。

G4传递函数的导出

接着将计算输出的滤波器模块G4、。请看图4。

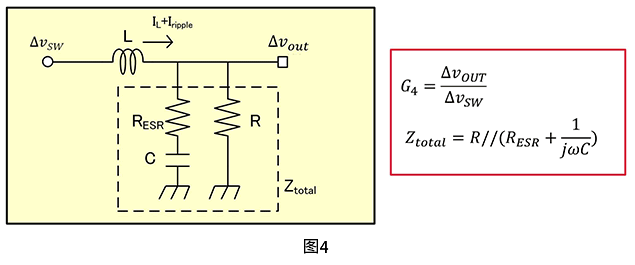
上图表示从VSW经过LC滤波器与Vout连接的路径。从VSW开始看，可以认为Vout是L和Ztotal的阻抗的阻抗划分，因此就可以导出以下公式4-2。

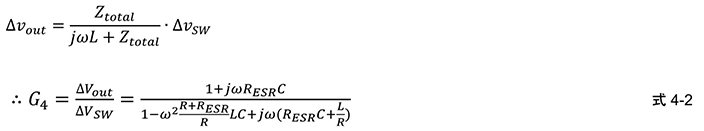
在这里，将在本G4的传递函数数基础上，考虑以下两种案例。

案例1

如果，RESR=0、R=open(∞) 的话，G4则变为如下。

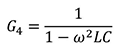
在经常见到的LC滤波器中，波特图如右图。这样的话，我想应该很快就能有印象。

f变小时，G4会变为正（＞0）值，因此Phase通常为0。

f变大时，变为的话，分母为0，因此Gain发散。

另外，f变大的话，G4会变为负（＜0）值，因此Phase将180°旋转。

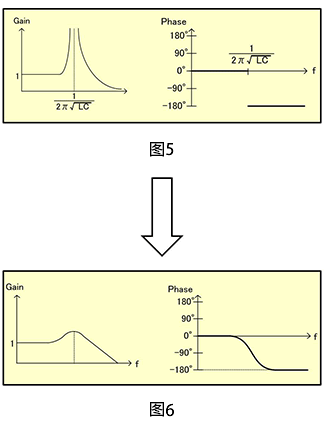
案例2

在案例1增加RESR和R，分母则加上1次虚数项。特别小或者特别大时，虽然和案例1相同，但是在f的谐振点附近，分母不会变为0，因此Gain不发散。

此时，在这里还残留着1次虚数项，因此相位不会0→180°，而是0→90°→180°这样变化。用波特图表示这一过程的就是图6。

G4的传递函数和波特图的关联，现在能有点印象了。

TOTAL传递函数（降压电压模式一般公式）

从这里开始将结合目前为止导出的传递函数，计算出作为整体的TOTAL传递函数。TOTAL的传递函数之前已介绍过，可以用以下公式来表示。

在此公式基础上，G可以写成如下形式。

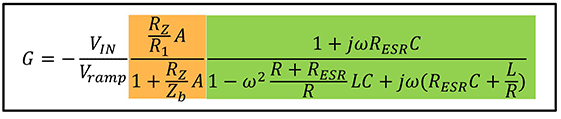
本公式的波特图如图7所示，可以看出各模块特征。并用不同的颜色表示各公式和图表的各区框。

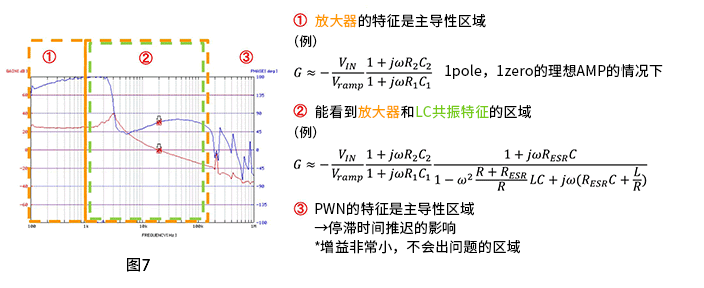
像这样根据每个模块来描述制作传递函数公式的话，就可以画出系统的波特图。但是，目前为止的论述都是先以有印象为主简单描述，因此会有不是很严密的部分。那是，G3和G4的导出部分，这种思路可适用于降压模式，但是却不适用于升压及升降压模式。因此，需要能适应这些所有的模式，状态平均化的思路。