EEPW论坛

要很好地了解功率因数，必须理解它与交流电之间的关系。可以将功率因数视为“功率三角形”。在功率三角形中，三边分别表示有功功率、无功功率和视在功率。
上述示例在功率三角形中表示如下：

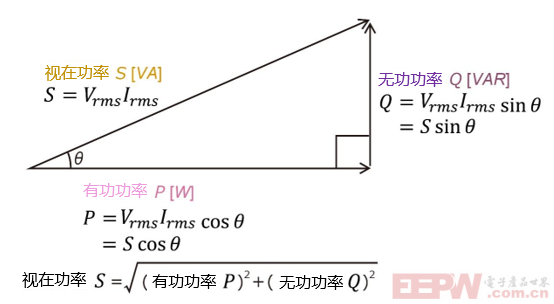
要很好地了解功率因数，理解它与交流电之间的关系至关重要。可以将功率因数视为“功率三角形”。在功率三角形中，三边分别表示有功功率、无功功率以及视在功率。

上述示例在功率三角形中表示如下：

功率三角形是直角三角形，其斜边表示视在功率S ，底边表示有功功率P，高度表示无功功率Q。每条边的长度定义如下：

・视在功率

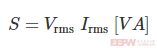
其中，Vrms是电压的有效值，Irms是电流的有效值。

・有功功率

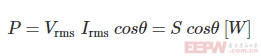
其中，θ表示电压和电流之间的相位差。

・无功功率

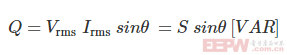
如果将这些关系直观地用一个“三角形”来看，可以得到以下三角关系：

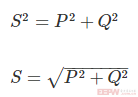
・功率因数
功率因数 cosθ用有功功率P 与视在功率S之比来表示。

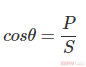
功率因数越接近1，意味着负载越接近理想的阻性负载，功率传输效率越高。相反，如果功率因数低，则意味着负载消耗了更多的无功功率，供电效率降低。