EEPW论坛

传统的正交下变频是通过对模拟I、Q输出直接采样数字化来实现的，由于I、Q两路模拟乘法器、低通模拟器本身的不一致性、不稳定性，使I、Q通道很难达到一致，并且零漂比较大，长期稳定性不好，不能满足高性能电子战设备的要求。为此，人们提出了对中频信号直接采样，经过混频来实现正交数字下变频的方案，这种下变频的方法可以实现很高精度的正交混频，能满足高镜频抑制的要求。采用可编程器件FPGA对该算法流程进行实现，能满足在高采样率下的信号时实处理要求，在电子战领域中有着重要的意义。

1 、数字正交混频变换原理

所谓数字正交混频变换实际上就是先对模拟信号x（t）通过A／D采样数宁化后形成数字化序列x（n），然后与2个正交本振序列cos（ω0n）和sin（ω0n）相乘，再通过数字低通滤波来实现，如图1所示。

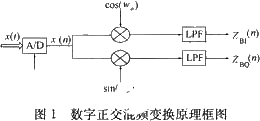
为了能够详细地阐述该算法的FPGA实现流程，本文将用一个具体的设计实例，给出2种不同的实现方法（不同的FPGA内部模块结构），比较其优劣，最后给出结论。该设计是对输入信号为中频70 MHz，带宽20 MHz的线性调频信号做数字正交混频变换，本振频率为70 MHz（即图1中的2个本振序列分别为cos（2π70Mn）和sin（2π70Mn）），将其中频搬移到0 MHz，分成实部（real）和虚部（imag）2路信号。然后对该2路信号做低通滤波，最后分别做1／8抽取输出。结构如图2所示。

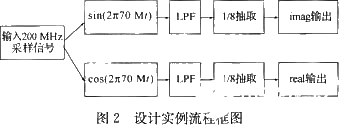
根据其算法流程在MATLAB下进行仿真（低通滤波器用切比雪夫一致逼近法进行设计，过渡带为10M～45M，阶数为23），最后2路输出波形如图3所示。

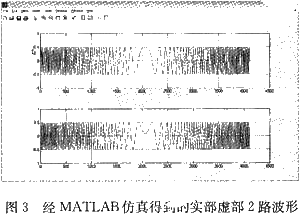
2 、基于FPGA的常规实现方法

首先用A／D芯片对输入信号进行实时采样，将数据量化为12位有符号数（最高位为符号位）。对于imag和real两路中的其中一个通道而言，乘本振序列模块可用一个16×16的有符号乘法器及一个32×16位的只读ROM实现。因为时钟频率为200 MHz，对于序列cos（2π70Mn）和sin（2π70Mn）只需要在ROM中存20个点就可以成为一个周期，固ROM的数据深度选32，宽度选16。滤波模块实质是一个“乘累加”结构，23阶的LPF须配置24个乘法器和20个加法器。最后抽取只需在滤波模块输出后每8个点取一个点。

根据这样的流程在ISE下编写代码，并用Modelsim仿真。

图4中共有4路输出波形，其中上2路分别为滤波后抽取之前的实部和虚部的输出，数据频率为200 MHz；而下面2路分别为1／8抽取后的实部和虚部的输出，数据频率为200／8=25 MHz。

对上述实现方法的评价：该方法完全按照算法的流程，结构比较清晰，容易理解，也能够最后得到理想的波形。但具有一定的弊端，主要有以下2点：（1）资源耗费太大，该种实现方式实部，虚部通道各需要24个乘法器和20个左右的加法器；（2）难以满足信号实时处理要求的运算速度。对于该方法，流程中所需要的乘法器和加法器都必须工作在200 MHz时钟下，这对于现有的硬件设备（如VertexⅡ）来讲是难以实现的，故需要采用更优化的实现方法，即下面所要介绍的多相滤波结构。

3 、运用多相滤波结构进行设计

对于上面所述的常规实现方法，之所以在合理性上存在一定弊端，归其原因是将FPGA大量的资源和运算周期都浪费在了不必要的运算点上。因为最后要得到的是时域信号的1／8抽取，即每8个点只保留一个点。因此大可以去寻找一种办法使得FPGA只计算需要的点即抽取后的点，直接以25 MHz的速度输出，这样既可以满足运算速度的要求，又能节省资源，这样的方法就是多相滤波的方式。

设数字滤波器（诸如内插，抽取器中的低通滤波器）的冲击响应为h（n），则其Z变换H（z）定义为：

对求和式展开可重写为：

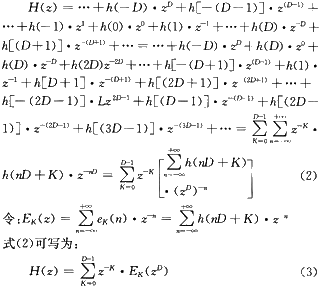
式（3）即为数字滤波器件H（z）的多相滤波结构，将其运用于抽取器，并且注意到抽取器的等效关系，则本设计FPGA内部（其中一个通道）可用图5所示的结构进行设计。

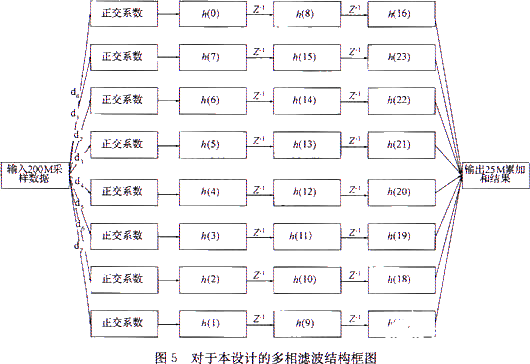
如图5所示，在200 MHz的时钟频率下，输入的采样数据以8点为周期依次打入8个通道，这样每个通道中的数据周期为200／8=25 MHz。数据进入通道后首先要乘以正交系数，在本设计中正交sin和cos表各是以20个点为一个周期，必须按照一定的等效规律将20个点排到8个通道中去，考虑到5×8=40正好是2个周期，可令N=0～39，将所对应的40个正交系数分成5组用状态机的方式打入8个通道中去，然后做乘累加。这里仍然用长度为24的滤波器，也要按照一定的规律将24个滤波系数（3个一组，见图5）排列到8个通道中去，原则是要保证在任何时刻8个通道的累加和要完全等效于原方法流程中滤波后的1／8抽取（可以验证，上面的系数排列方式是满足这一要求的）。很显然，这样做后每个通道的时钟频率都是原来频率的1／8，并且数据是完全并行处理的。乘法器和加法器都工作在25 MHz时钟频率下，可以很容易实现，且程序更加高效和科学。

4、 进一步优化的方法

采用了多相滤波方式后，每个通道需要4个乘法器。一般情况下，乘法器的延迟大概是在7～10 ns。而在25 MHz时钟频率下，完全可以将乘法器进行复用，即在40 ns周期内完成4次乘法运，算包括1次乘正交系数，3次乘滤波系数。这样每个通道只需要一个乘法器就可以。于是整个设计中所需要的乘法器可以降为16个（实部、虚部各8个），加法器则需要46个（各23个）。

5 、最终仿真波形

根据上面的多相滤波思想，并采用乘法器复用，在ISE下编写VHDL代码，用Modelsim仿真得到最终的波形。

用Synplify进行综合布线后得到的资源报告如下（选用的器件是VertexⅡxc2v1000）：

6 、结束语

本文提出的基于FPGA的数字正交混频下变换的实现方法，对比了2种不同的设计方案以及相应的FPGA内部结构，分析了各自利弊；最后，着重介绍了其中效率较高并且较为科学的多相滤波结构。在做实时信号处理时，该结构能够使资源优化，并且满足运算速度的要求，实现起来也不复杂，在实际工程中有很强的运用价值。