过去半年有几位客户请我帮助他们设计和实现数字下变频器所用的降采样(即“抽取”)滤波器,这种滤波器在软件无线电与数据采集类应用中都很常见。这项工作即便对于经验丰富的设计师也不是一件小事。事实上,仅仅算出在FGPA中实现滤波器所需要的资源可能就是一个很大的问题。虽然MATLAB®(MathWorks 开发)具有用于滤波器设计与分析 (FDA) 的绝妙工具箱,但是它提供太多滤波器设计方法,会让新用户无从下手。另外,您必须能够根据DSP理论解释MATLAB命令产生的结果,仅仅这一点就需要研究。
抛开理论的细枝末节,让我们开始围绕上述问题探讨降采样有限脉冲响应 (FIR) 滤波器的设计与实现。本辅导资料实际上旨在向您介绍一种简便、易于理解的流程——从滤波器系数生成到FGPA目标器件中抽取滤波器的实现。所需工具只有MATLAB较新版本(本人仍在使用R2008a)及其FDA工具箱、以及ISE® 11.4套件提供的赛灵思CORE GeneratorTM工具。这些工具是设计多速率FIR滤波器的必备工具。
特别是我们将探讨固定降采样速率变化的两个实例:整数值与有理值。您应当能够把我们在本辅导资料介绍的MATLAB指令和CoreGen图形用户界面 (GUI) 设置应用到您的设计当中。为了说明公用逻辑块 (CLB) Slice 、18KB内存RAM块(BRAM) 和DSP48乘法累加 (MAC) 单元等方面的资源占用情况,我们将采用 XC6VLX75T-2ff484 作为目标 FPGA 器件。
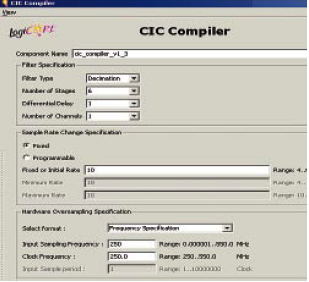
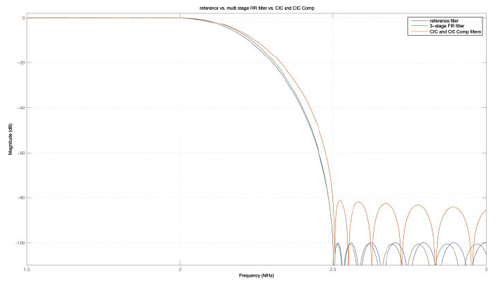
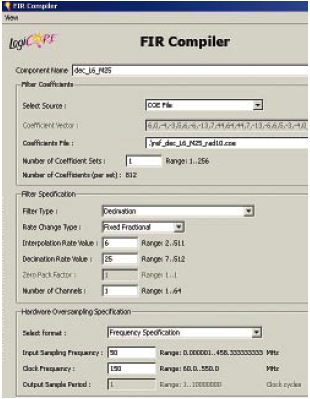
整数倍降采样器假设基带中进行解调后按250MHz速率传输带宽只有2.5MHz的信号。我们必须过滤从2.5MHz到 250MHz 的所有频率,因为它们不传输任何有用信息;这正是我们准备设计和实现的低通 FIR 滤波器的目的。根据尼奎斯特定理,输出数据速率是信号带宽的两倍;因此,我们需要按照M=50的整数倍对其执行降采样。我将介绍两种采用多级滤波方法的可行备选实现方案:第一种方法采用三个串联的 FIR 抽取滤波器,而第二种方法则同时采用级联积分梳状 (CIC) 滤波器与FIR滤波器。
以下是用于设计理想滤波器的MATLAB代码。我们假设通带和阻带频率的衰减分别为0.1dB和100dB。

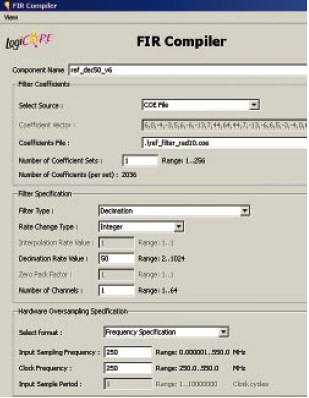
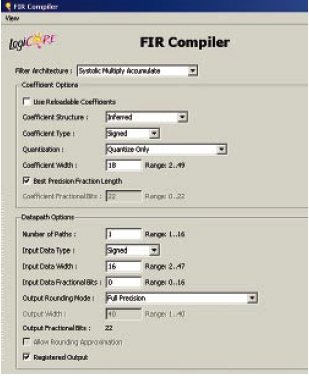
假设FPGA时钟频率Fclk=Fs_in,那么在Virtex®-6器件中我们需要多少个DSP48 MAC单元?它是用于按M进行降采样的滤波器。根据FIR Complier 5.0数据手册 (fir_compiler_ds534.pdf) 详细阐述的理论,我们可以把DSP48 MAC分成M个相位,因此引入“多相”这一术语。由于每个相位都是按更低的输出频率 Fs_out 进行处理,因此可以按时分复用方式共享DSP48 MAC。以下理论计算表明,FIR-Compiler在通过多相分解方式实现滤波器时采用最小的22个MAC单元(total_num_MAC_ref )。滤波器长度是2100 (total_num_coeff),填写0成为M的整数倍。请注意:此方案考虑系数对称性。


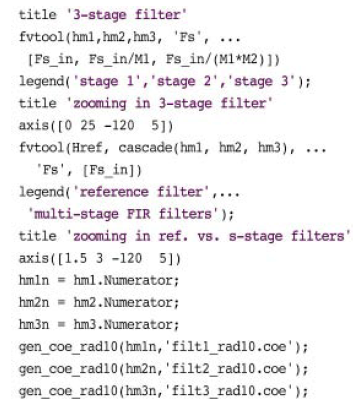
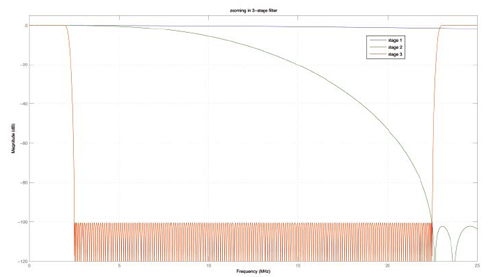
在MATLAB中可以轻松按低通滤波建立抽取过程模型,然后按M降采样,最终分别产生y与y_filt输出信号。不过,在FPGA器件中,这种实现方式效率不高:它会很笨地计算随后必须抛弃的值。相反,多相抽取器把输入信号降采样到M个wk通道,每个通道由其自身的子滤波器ph(k,:) 过滤。部分结果y_out(k,:) 然后汇总在一起组成最终输出y_tot。把y_tot与本机MATLAB指令产生的基准 y 对比,结果表明最终输出均处于数值精度3e-15范围内(由于不同运算阶数而出现偏差)。
















 我要赚赏金
我要赚赏金

