波特图,作为模拟电子电路中的一个重要知识点,相信很多朋友都没有特别注意过,只关注过3dB带宽,6dB带宽之类的名词。书上也经常说该系统的传递函数是什么什么,波特图为什么,让人没有心情继续看下去。其实,作为电子工程师,如果写出一个系统的传递函数,大致画出该系统的波特图,就能大致分析系统的稳定性,对系统的性能有一总体的印象。这篇文章我带领大家对系统的波特图进行分析,从“艺术”的眼光分析下波特图的魅力所在。
本文引用地址:http://www.eepw.com.cn/article/170177.htm
波特图是线性时不变传递函数对频率的半对数座标图,其横轴表示频率,纵轴表示幅度,我们可以利用波德图可以看出系统的频率响应。波德图一般是由二张图组合而成,一张幅频图,表示频率响应增益的分贝值对频率的变化,另一张相频图,是频率响应的相位对频率的变化。

现在以一简单的低通滤波器来窥探下波特图的魅力。
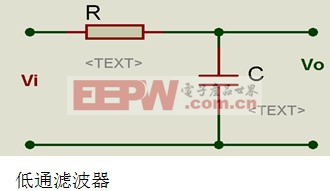
传递函数

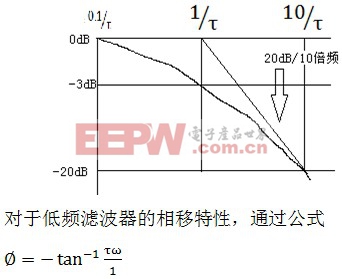
我们将该点叫做频率转折点,在频率较低的范围内,增益大约为1,在频率较高的范围内,系统增益以-20dB/10倍频的速度下降。在滤波器设计中,也就是我们常听到的3dB带宽的截止频率。低通滤波器的波特图频率响应部分如下所示:

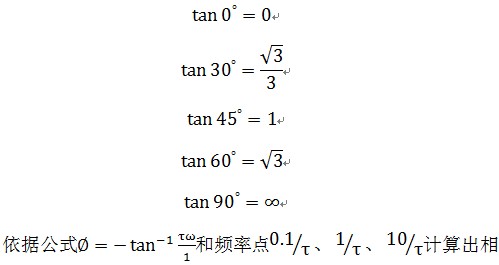
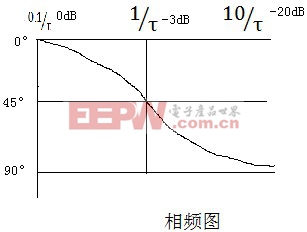
 我要赚赏金
我要赚赏金

