EEPW论坛

　　摘要

　　是否曾想过为什么一个设计能够以高于设计团队承诺的频率工作?为何该设计团队不能将这个更高的频率当作要实现的目标?

　　过去，静态时序分析被用来分析SoC是否能够在规定的目标频率工作。时序验收要么在最差情况(WCS)，要么在最佳情况(BCS)下完成。通常，这些与三西格玛区域对应。当然，为了结束这些情况下的时序，可能进行了大量过度设计。

　　统计静态时序分析(SSTA)尝试采用一种方法来减少这种不必要的过度设计，因此努力让设计变得更加切合实际，并同时帮助提高目标频率。

　　什么是统计静态时序分析?

　　过去几十年里，静态时序分析(STA)一直是用来结束数字电路时序的一种常用方法。

　　但由于几何尺寸缩小到45nm甚至更小，现在要结束时序变得越来越困难了。STA和工艺数量的增加，使得整个情形变得更为复杂。

　　之所以出现这样的复杂情况，是因为要在高级技术节点上实现工艺变化变得异常困难了。现在共有两种变化：

　　1.芯片到芯片变化

　　2.芯片内变化

　　这两种变化又可以进一步划分为：

　　1.系统性变化

　　2.随机性变化

　　其中的部分变化目前仍算在传统的STA方法内。SSTA尝试按概率分布来考虑所有这些变化。

　　基本上，SSTA会计算概率函数，以计算每个节点上每个信号的到达时间。如果设计达到规定的目标频率，根据到达时间的概率分布函数，就能将它计算出来。

　　例如，如果概率为97%，那么最小余量的信号的到达时间为5ns;到达时间为4ns的概率为10%。这意味着200MHz的目标频率其得到的概率应为97%，250MHz的目标频率其概率为10%。

　　变化：

　　临界尺寸的扩展速度超过了我们的控制。现在随着技术节点的减少，互连变化与有源门相比，它正逐渐占据主导地位。

　　由于互连开始占主导地位，时序的临界变量不只限于晶体管的临界尺寸，同时包括线段尺寸和实际形状以及附近网络的数量。

　　金属宽度、金属厚度、经电阻、绝缘高度都具有不同的金属层属性。晶体管的类似属性包括晶体管长度、宽度、掺杂密度和门氧化层厚度。

　　1.互连变化

　　这种统计法对互连领域里所有可能的变化组合建模型。例如，启动路径可能位于金属3中，而获取路径就能够则位于金属4中。

　　过去，STA在所有金属中会各不相同，因此不能将金属3导致最大时延、金属4导致最低时延的这种情况设立模型。此类组合对应于建立路径的最差情况，只能从统计角度对互连变化建模来获取。

　　2.芯片内变化：

　　目前，这是通过使用启发式降额数，以及对最差情况和最佳情况时序模型进行片上变化分析来完成的。

　　3.芯片间变化：

　　工艺参数存在变化，这可能以类似方式对所有芯片产生影响。在STA中，这是通过WCS时序模型(慢晶体管)和BCS时序模型(快晶体管)来处理的。

　　概率密度函数(PDF)

　　在SSTA中，所有参数(随机和系统参数)都是按概率分布函数(PDF)的角度来处理。

　　即使用的不是单个值，而是概率密度函数。下面的图1给出了PDF示例。

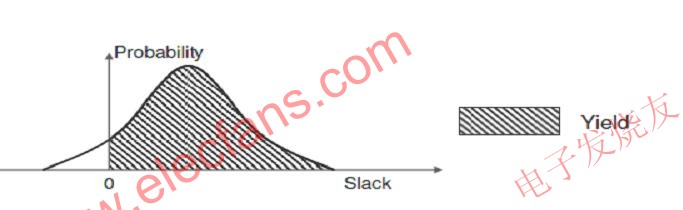
　　图1：余量的概率密度函数(PDF)

　　时序路径举例：

　　下面给出了时序路径的一个例子(图2)。时序路径的PDF如下图所示(图3)。这个PDF是通过对门时延PDF和到达时间统计分析后计算得到的。

　　到达时间、余量、压摆等都采用Taylor系列仪器计算得出。

　　a0+∑i=1,n(aiGi)+an+1Ra

　　其中，

　　–a0是平均值

　　–Gi是“n”全局源变化

　　–ai描述对应Gi的统计变化

　　–Ra是独立随机变量R的变化

　　–an+1描述对应Ra的统计变化。

　　平均值(µ)=a0+∑i=1,nai平均值(Gi)+an+1平均值(Ra)------(i)

　　标准差(σ)=[aiStd(Gi)2+an+1Std(Ra)2]½-(ii)

　　使用上面两个等式，这些分布函数可以用如下方式表示：

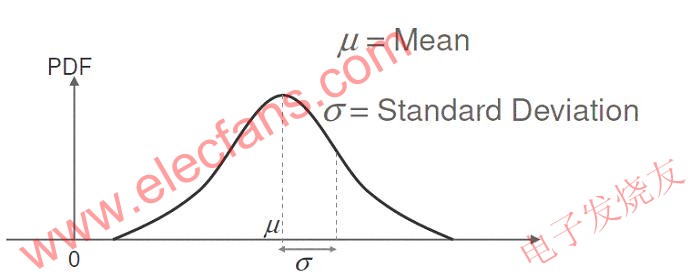
　　图2：PDF示例

　　门时延的PDF(红色)和到达时间(绿色)也在图3中标记出来了。

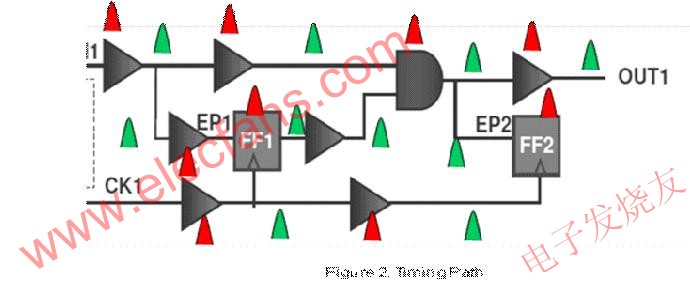
　　图3：时序路径

　　OUT1的PDF：

　　所示区域代表违反时序的概率。基本上，该区域代表当前目标频率产生的损失。该PDF还对第1段提到的问题做了回答。现在，设计人员可以声称频率数字考虑了结果平衡。这种情况有助于提高设计公司的利润，因为它们可以声称能够实现更接近的目标频率。

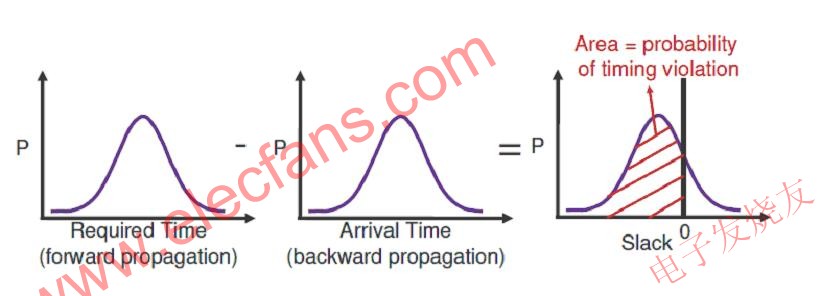
　　图4：时序路径的PDF

　　如上图所示，规定时序时间和达到时间的PDF结合起来，计算分布情况。要注意的另一个方面是，在达到上图(图4)所示的数字之前，时钟延迟也可以用统计方式表示。

　　SSTA–难点

　　1.概率函数很难计算。更重要的是，从统计角度看芯片上的变化不是彼此独立的。

　　2.计算需要S–lib格式的时序模型。

　　3.由于统计数据容量大，与传统的STA相比，该计算属于内存密集型。

　　4.运行时间也是一个难点。

　　但是，只要记住SSTA能为设计团队提供的优势，所有这些难点都可以迎刃而解。

　　总结

　　与传统的STA相比，SSTA仍处于初期阶段，但它能以更切实可行的方式为设计提供收尾工作。它根据工艺和互连参数变化，对设计进行分析。