EEPW论坛

反馈振荡器的原理

一、反馈振荡器的原理分析
1、反馈振荡器的组成
反馈振荡器由放大器和反馈网络两大部分组成。
反馈型振荡器的原理框图如图4-1所示。由图可见, 反馈型振荡器是由放大器和反馈网络组成的一个闭合环路, 放大器通常是以某种选频网络(如振荡回路)作负载, 是一调谐放大器, 反馈网络一般是由无源器件组成的线性网络。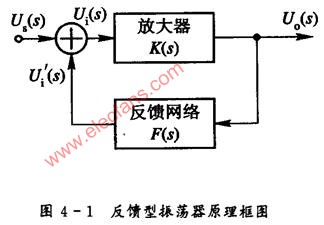

2、自激振荡的条件分析

自激振荡的条件：就是环路增益为1, 即

二、平衡条件
根据前面分析，振荡器的平衡条件即为

值得说明的是：
（1）平衡时电源供给的能量等于环路消耗的能量；
（2）通常环路只在某一特定才满足相位条件。

三、起振条件
为了使振荡过程中输出幅度不断增加, 应使反馈回来的信号比输入到放大器的信号大, 即振荡开始时应为增幅振荡, 因而由式(4-8)可知

式(4-16a)和(4-16b)分别称为起振的振幅条件和相位条件, 其中起振的相位条件即为正反馈条件。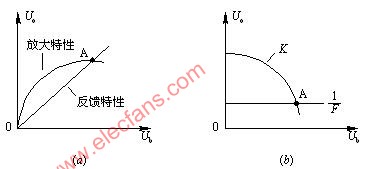

图 4-2 振幅条件的图解表示
起振过程：开始增幅振荡 非线性 稳幅振荡
四、稳定条件
1、振荡器稳定概念的提出：
2、振荡器的稳定条件
振荡器的稳定条件分为振幅稳定条件和相位稳定条件。
(1) 振幅稳定条件
要使振幅稳定，振荡器在其平衡点必须具有阻止振幅变化的能力。具体来说，就是在平衡点附近，当不稳定因素使振幅增大时，环路增益将减小，从而使振幅减小。
振幅稳定条件为：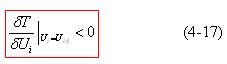

由于反馈网络为线性网络, 即反馈系数大小F不随输入信号改变, 故振幅稳定条件又可写为

(2)、相位稳定条件
我们知道，一个正弦信号的相位φ和它的频率ω之间的关系：

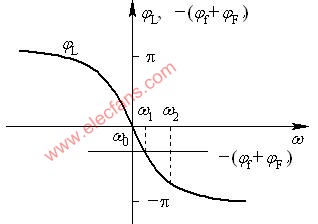
图 4-4 互感耦合振荡器

五、振荡线路举例——互感耦合振荡器
图4-4是一LC振荡器的实际电路, 图中反馈网络由L和L1间的互感M担任, 因而称为互感耦合式的反馈振荡器, 或称为变压器耦合振荡器。
分析教材图4-4的正反馈过程。