EEPW论坛

　　既然一个数可以用二进制和十进制两种不同形式来表示，那么两着之间就必然有一定的转换关系。
　　由十进制数的一般表示式：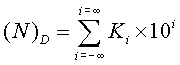
　　可以得到整数的一般表达式：

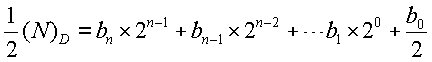
　　将等式两边分别除以2，可得第一个余数b0，同时上式演变为：

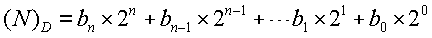
　　将等式两边再除以2，可得第二个余数b1，等式变为：

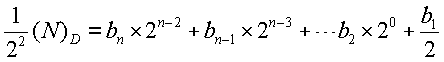
　　重复上述过程直到商为0，就可由所有的余数求出二进制数。

　　例题 1.3.3 将(25)_D转换为二进制数。
　　解：该题的解题思想是，不断地用2分解十进制整数，并将余数按得到的顺序由低位到高位排列，即可得到对应的二进制数。

　　所以(18)_D＝(b₄ b₃ b₂ b₁ b₀)_B＝(10010)_B
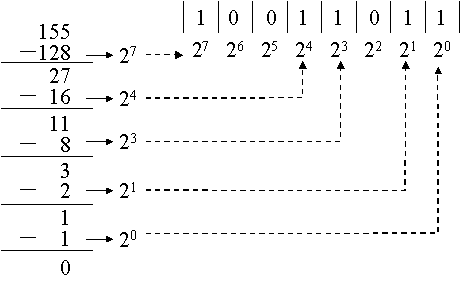
　　例题1.3.4 将(155)_D转换为二进制数解：当要将一个很大的十进制数转换成二进制数时，采用例题1.3.3的做法很费时 ，我们可以采用另外一种方法。这种方法的思想是从需要转换的十进制数找到与之最接近的2的幂次方，并从这个十进制数中减去该2的幂次方，在剩下的余数中重复这种做法，直到余数为0。然后将所得到的这些2的幂次方与二进制数中的位权相比，相同的位标记为1，其余的为0，这样就可得到与十进制数对应的二进制数。
　　现在我们来看看155这个十进制数，与2的各个幂次方数比较后可知，与155最近的是128，即2⁷，155减去128后余数为27，而27最接近的是2⁴，27减去16得到11，11减去8（2³）得到3，3减去2（2¹）得到1，1减去1（2⁰）得到0。由于在本次计算中得到2的最高幂次为7，因此可以得知对应的二进制数是一个八位的二进制数，写出这个二进制数的位权，并将其与得到的五个2的幂次方数对比后填入1，其余的用
0代替，最后得到的二进制数为10011011。

　　需要指出的是，多数计算机或数字系统中只处理4、8、16、32位的二进制数据，因此,数据的位数需配成规格化的位数，如例题1.3.3种转换结果为11001，如将它配成8位,则相应的高幂项应填以0，其值不变，即11001=00011001。
　　根据十进制数的一般表达式，可以得到十进制小数的表达式如下
：

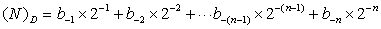
　　将等式两边分别乘以2，可得：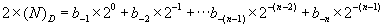

　　比较上面两式，可以发现第一项中2的幂次已经由原来的-1变成了0，而2⁰是整数的最低位的位权，因此可以将该项从表达式中去掉，也就是去掉了b_-1。，这样也就使得剩下的数保持为纯小数。继续在表达式的两端乘以2，可得：
　　这样又得到了一个2⁰项，也就是b_-2也将再次被从式子中剔除，但同时也就产生了二进制小数的前两位。重复上述过程，直到 满足要求的位数时做“四舍五入”，也就完成了从十进制小数到二进制小数的转换。
　　例题8：将(0.706)_D转换成误差ε不大于2^-10二进制小数。
解：
　　0.706 ×2=1.412……1……b_-1
　　0.412 ×2=0.824……0……b_-2
　　0.824 ×2=1.648……1……b_-3
　　0.648 ×2=1.296……1……b_-4
　　0.296 ×2=0.592……0……b_-5
　　0.592 ×2=1.184……1……b_-6
　　0.184 ×2=0.368……0……b_-7
　　0.368 ×2=0.736……0……b_-8
　　0.736 ×2=1.472……1……b_-9

　　最后一位小数0.472小于0.5，根据“四舍五入”原则，则有：
0.0 ×2=0……0……b_-10

所以, (0.706)_D=(0.101101001)_B，误差ε 2^-10