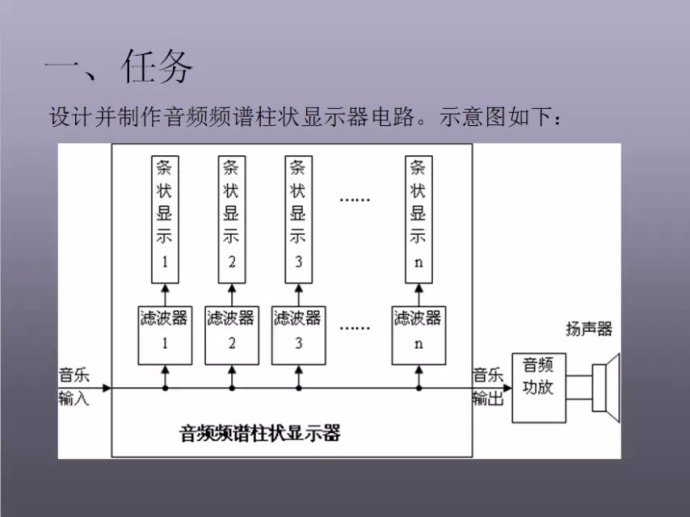
图1 2011年电子设计竞赛初赛题目
第二年老师重新布置任务,我接到的还是继续完成这个题目,硬件部分的滤波器倒是做好了,并且龙富做好了后期的显示条部分,但因期末考试的原因没能把硬件结合起来。
前些天翻了一下以前的笔记本,一幕幕记忆弥漫出来 。刚好有点时间,整理一下思路,决定用FFT算法去实现这个功能。 FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。想想《高数》、《复变函数》、《信号系统》、《现代自动控制系统》、《离散自动控制》都有涉及到,也算是专业知识了,今天就用它来实现多通道带通滤波器的数据解析。
本设计是基于单片机C的FFT快速傅里叶变换, 用于音频信号分析的一个典型音频频谱显示仪。整体实现框图如下:
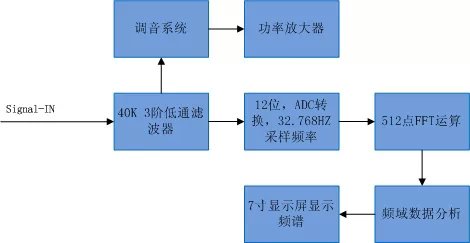
图2 整体框架 MCU控制部分使用32位ARM单片机,7寸TFT彩屏显示器 ,FFT算法使用纯C代码实现。整个实现过程中关键的一部分是数据的采样,为了完整的采样到32768HZ的音频信号,采用定时器触发ADC,并使用DMA传送到指定内存区域,再进行FFT运算。几天的FFT学习和数据分析,终于理解了整个功能的实现过程。
关键部分的是FFT核心转换程序,整理如下(声明:代码摘自网上):
FFT.h头文件
// 快速福利叶变换C函数
//函数简介:此函数是通用的快速傅里叶变换C语言函数,移植性强,以下部分不依
// 赖硬件。此函数采用联合体的形式表示一个复数,输入为自然顺序的复
// 数(输入实数是可令复数虚部为0),输出为经过FFT变换的自然顺序的
// 复数
//使用说明:使用此函数只需更改宏定义FFT_N的值即可实现点数的改变,FFT_N的
// 应该为2的N次方,不满足此条件时应在后面补0
//函数调用:FFT(s);
//时 间:2010-2-20
//版 本:Ver1.0
//参考文献:
#ifndef __FFT_H
#define __FFT_H
#include "math.h"
#define PI 3.1415926535897932384626433832795028841971//定义圆周率值
#define FFT_N512 //定义福利叶变换的点数
struct compx {floatreal,imag;}; //定义一个复数结构
extern struct compxs[FFT_N]; //FFT输入和输出:从S[1]开始存放,根据大小自己定义
void FFT(struct compx*xin); //FFT核心算法
#endif
FFT.c文件:
#include "FFT.h"
struct compx s[FFT_N];//FFT输入和输出:从S[1]开始存放,根据大小自己定义
struct compx EE(struct compx a,struct compxb)
{
struct compx c;
c.real=a.real*b.real-a.imag*b.imag;
c.imag=a.real*b.imag+a.imag*b.real;
return(c);
}
void FFT(struct compx *xin)
{
int f,m,nv2,nm1,i,k,l,j=0;
struct compx u,w,t;
nv2=FFT_N/2; //变址运算,即把自然顺序变成倒位序,采用雷德算法
nm1=FFT_N-1;
for(i=0;i
{
if(i
{
t=xin[j];
xin[j]=xin[ i];
xin[ i]=t;
}
k=nv2; //求j的下一个倒位序
while(k<=j) //如果k<=j,表示j的最高位为1
{
j=j-k; //把最高位变成0
k=k/2; //k/2,比较次高位,依次类推,逐个比较,直到某个位为0
}
j=j+k; //把0改为1
}
{
intle,lei,ip; //FFT运算核,使用蝶形运算完成FFT运算
f=FFT_N;
for(l=1;(f=f/2)!=1;l++) //计算l的值,即计算蝶形级数
;
for(m=1;m<=l;m++) // 控制蝶形结级数
{ //m表示第m级蝶形,l为蝶形级总数l=log(2)N
le=2<<(m-1); //le蝶形结距离,即第m级蝶形的蝶形结相距le点
lei=le/2; //同一蝶形结中参加运算的两点的距离
u.real=1.0; //u为蝶形结运算系数,初始值为1
u.imag=0.0;
w.real=cos(PI/lei); //w为系数商,即当前系数与前一个系数的商
w.imag=-sin(PI/lei);
for(j=0;j<=lei-1;j++) //控制计算不同种蝶形结,即计算系数不同的蝶形结
{
for(i=j;i<=FFT_N-1;i=i+le) //控制同一蝶形结运算,即计算系数相同蝶形结
{
ip=i+lei; //i,ip分别表示参加蝶形运算的两个节点
t=EE(xin[ip],u); //蝶形运算,详见公式
xin[ip].real=xin[ i].real-t.real;
xin[ip].imag=xin[ i].imag-t.imag;
xin[ i].real=xin[ i].real+t.real;
xin[ i].imag=xin[ i].imag+t.imag;
}
u=EE(u,w); //改变系数,进行下一个蝶形运算
}
}
}
}
FFT分析后的数据虽然有一定的规律,但是还不能满足频谱显示的需求,需在程序控制上针对显示器的尺寸进行数据放缩,顶值限幅等才能输出酷炫的FFT频谱界面。
汗水终究交换了成功,FFT频谱显示,如图:
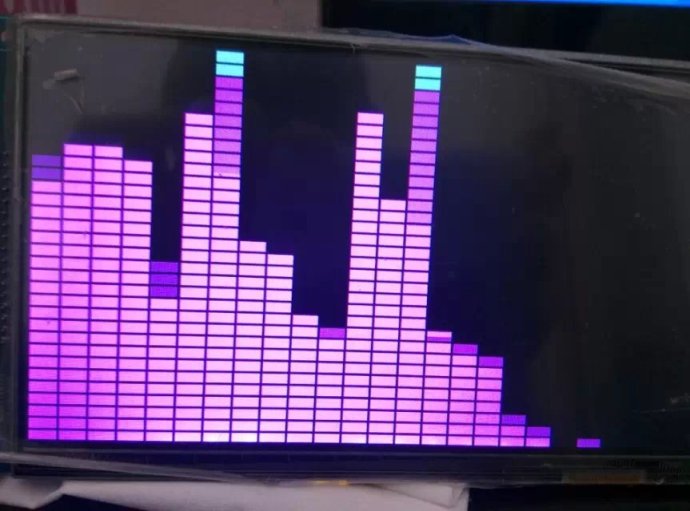
图3 FFT普显示1
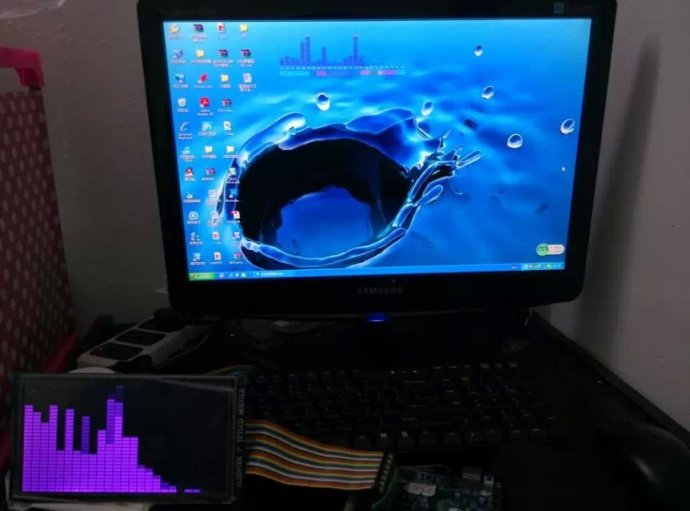
图4 FFT普显示2
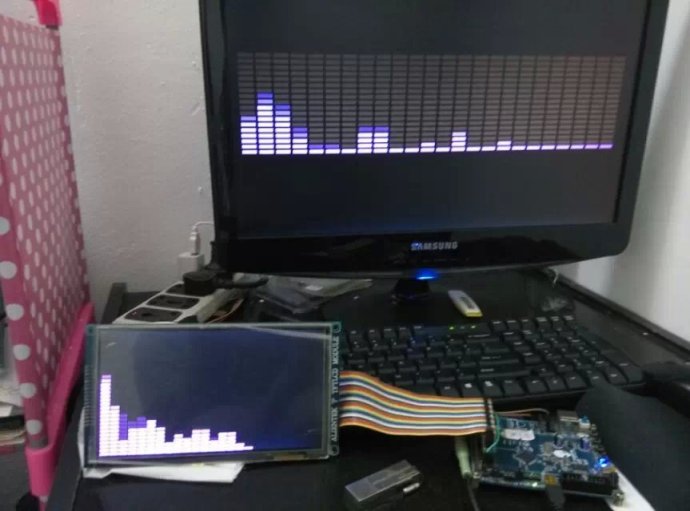
图5 FFT普显示3

图6 FFT普显示4

 我要赚赏金
我要赚赏金

