EEPW论坛

MEMS加速度计已经比传统振动传感器（尺寸，重量，成本，抗冲击性，易用性）所具有的许多优势，促使MEMS加速度计在新兴条件下的使用 - 基于监测（CBM）的系统。因此，许多CBM系统架构师，开发人员甚至他们的客户都是第一次考虑这些类型的传感器。很多时候，他们面临着快速学习如何评估MEMS加速度计测量其机器平台上最重要的振动属性的能力的问题。

这可能看起来很难，因为MEMS加速度计数据表通常表达了这些开发人员可能不熟悉的最重要的性能属性。例如，许多人熟悉用线速度（mm / s）来量化振动，而大多数MEMS加速度计数据表用重力参考加速度（g）表示它们的性能指标。幸运的是，有一些简单的技术可以实现从加速到速度的转换，以及估计关键加速度计行为（频率响应，测量范围，噪声密度）对重要系统级标准（带宽，平坦度，峰值振动，解析度）。

基本振动属性

该过程首先从惯性运动的角度回顾线性振动。在这种情况下，振动是一种机械振荡，其平均位移为零。对于那些不希望他们的机器在工厂车间移动的人来说，零平均位移非常重要！振动传感节点中的核心传感器的值将直接与其表示机器振动的最重要属性的程度相关。为了开始评估特定MEMS加速度计在这种能力下的能力，重要的是从惯性运动的角度对振动的基本理解开始。

图1提供了振动运动曲线的物理图示，其中灰色框表示中点，蓝色图像表示一个方向上的峰值位移，红色图像表示另一个方向上的峰值位移。等式1提供了一个数学模型，该模型描述矩形物体在一个频率（f V）振动时的瞬时加速度，其幅度为A rms。

图1.简单的线性振动运动。

公式1

在大多数CBM应用中，机器平台上的振动通常会比公式1中的模型具有更复杂的光谱特征，但是该模型在发现过程中提供了一个很好的起点，因为它确定了CBM系统的两个常见振动属性。经常跟踪：幅度和频率。这种方法在将关键行为转换为线速度方面也很有用（稍后将详细介绍）。图2提供了两种不同类型的振动曲线的光谱图。第一个配置文件（参见图2中的蓝线）在其频率范围内具有恒定的幅度，该频率范围在f 1  和f 6之间。第二个轮廓（见图2中的绿线）在四个不同频率上具有峰值：f 2，f3，f 4和f 5。

图2. CM振动曲线示例。

系统要求

测量范围，频率范围（带宽）和分辨率是通常量化振动感测节点能力的三个常见属性。图2中的红色虚线通过一个矩形框来说明这些属性，该框由最小频率（f MIN），最大频率（f MAX），MIN），最大频率（f MAX），最小幅度（A MIN），和最大幅度（A MAX）。当考虑将MEMS加速度计用于核心传感器在振动传感节点中的作用时，系统架构师可能希望在其设计周期的早期分析其频率响应，测量范围和噪声行为。

有一些简单的技术可用于评估这些加速度计行为，以预测加速度计对一组给定要求的适用性。显然，系统架构师最终需要通过实际验证和认证来验证这些估算，但即使这些努力也会重视早期分析和加速度计功能预测所带来的期望。

频率响应

公式2给出了一个简单的一阶模型，该模型描述了MEMS加速度计在时域中对线性加速度（a）的响应（y）。在这种关系中，偏差（b）表示传感器在经历零线性振动（或任何类型的线性加速度）时的输出值。比例因子（K A）表示相对于线性加速度（a）的变化，MEMS加速度计的响应（y）的变化量。 

公式2

传感器的频率响应描述了比例因子（K A）相对于频率的值。在MEMS加速度计中，频率响应有两个主要因素：（1）其机械结构的响应和（2）滤波器在其信号链中的响应。公式3给出了一个通用的二阶模型，它给出了MEMS加速度计对频率响应的机械部分的近似值。在该模型中，fO表示谐振频率，Q表示品质因数。

公式3

信号链的贡献通常取决于应用程序所需的过滤。一些MEMS加速度计使用单极低通滤波器来帮助降低谐振频率下的响应增益。公式4提供了与此类滤波器（H SC）相关的频率响应的通用模型。在这种类型的滤波器模型中，截止频率（f C）表示输出信号的幅度低于其输入信号的频率√2。

公式4

公式5结合了机械结构（H M）和信号链（H SC）的贡献。

公式5

图3提供了该模型的直接应用，用于预测ADXL356的频率响应（x轴）。该模型假定标称谐振频率为5500 Hz，Q为17，并使用截止频率为1500 Hz的单极低通滤波器。请注意，公式5和图4仅描述了传感器的响应。该模型不包括考虑加速度计与其监控的平台耦合的方式。

图3. ADXL356频率响应。

带宽与平坦度

在利用单极低通滤波器（如公式4中的那个）建立频率响应的信号链中，其带宽规格通常可识别其输出信号输出功率的50％的频率信号。在更复杂的响应中，例如来自等式5和图3的三阶模型，带宽规范通常会带有平坦度属性的相应规范。平坦度属性描述了频率范围（带宽）上比例因子的变化。使用图3和公式5中的ADXL356仿真，1000 Hz时的平坦度约为17％，2000 Hz时的平坦度约为40％。  

虽然许多应用程序由于其平坦性（准确性）要求而需要限制它们可以使用的带宽，但是有些情况可能并不那么令人担忧。例如，某些应用程序可能更侧重于跟踪一段时间内的相对变化，而不是绝对准确性。另一个例子可能来自那些将利用数字后处理技术消除他们最感兴趣的频率范围内的纹波的人。在这些情况下，响应的可重复性和稳定性通常比响应的平坦度更重要。给定频率范围。

测量范围

MEMS加速度计的测量范围度量表示传感器可以在其输出信号中跟踪的最大线性加速度。在某个超出额定测量范围的线性加速度水平下，传感器的输出信号将饱和。当发生这种情况时，它会引入显着的失真，并且很难（如果不是不可能的话）从测量中提取有用的信息。因此，确保MEMS加速度计支持峰值加速度水平非常重要（参见 图2中的A MAX）。 

请注意，测量范围将依赖于频率，因为传感器的机械响应会在响应中引入一些增益，增益响应的峰值发生在谐振频率。对于ADXL356的模拟响应（参见图3），增益峰值约为4倍，从而将测量范围从±40 g降至±10 g。公式6提供了一种分析方法来预测这个相同的数字，使用公式5作为起点：

公式6

比例因子的巨大变化和测量范围的减小是大多数CBM系统希望将其振动暴露的最大频率限制在远低于传感器谐振频率的水平的两个原因。

解析度

“仪器的分辨率可以定义为环境中最小的变化，导致仪器指示发生可检测的变化。” 1  在振动传感节点中，加速度测量中的噪声将直接影响其能力。检测振动的变化（又名“分辨率”）。因此，对于那些正在考虑使用MEMS加速度计来检测机器平台振动的微小变化的人来说，噪声行为是一个重要的考虑因素。公式7提供了一个简单的关系，用于量化MEMS加速度计噪声对其解决振动微小变化的能力的影响。在此模型中，传感器的输出信号（yM）等于其噪声之和（N）和它正在经历的振动（V）。由于噪声（a N）和振动（a V）之间不存在相关性，传感器输出信号（| y M |）的大小将等于噪声幅度的根和平方（RSS）组合（| aN |）和振动的大小（| a V |）。

公式7

那么，需要什么级别的振动才能克服测量中的噪声负担并在传感器的输出信号中产生可观察到的响应？根据噪声水平量化振动水平可以帮助以分析方式探索这个问题。公式8通过比率（K VN）建立这种关系，然后根据该比率得出预测传感器输出变化水平的关系：

公式8

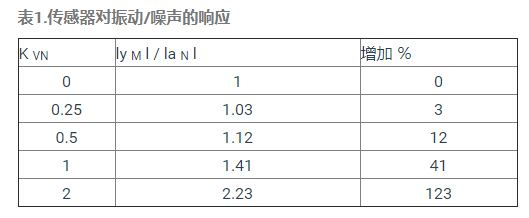
表1提供了这种关系的一些数值例子，以帮助说明传感器输出测量的增加，相对于振动和噪声幅度的比率（KVN）。为简单起见，本讨论的其余部分将假设传感器测量中的总噪声将确定其分辨率。从表1中，这涉及K VN  等于1的情况，即当振动幅度等于噪声幅度时。当发生这种情况时，当振动为零时，传感器输出的幅度将比其输出幅度增加42％。请注意，每个应用程序可能需要考虑在其系统中可观察到的增加级别，以便在该情况下为解决方案建立相关定义。

预测传感器噪声

图4显示了将使用MEMS加速度计的振动感测节点的简化信号链。在大多数情况下，低通滤波器为抗混叠提供了一些支持，而数字处理将在频率响应中提供更多定义的边界。通常，这些数字滤波器将寻求保持表示真实振动的信号内容，同时最小化带外噪声的影响。因此，在估计噪声带宽时，数字处理通常是系统中最有影响力的部分。这种类型的处理可以采用时域技术的形式，例如带通滤波器或通过频谱技术，例如快速傅里叶变换（FFT）。 

图4.振动传感节点的信号链。

等式9提供用于估计MEMS加速计的测量（A总噪声的简单关系NOISE），使用它的噪声密度（φ ND）和噪声带宽（F NBW与信号链相关联）。

公式9

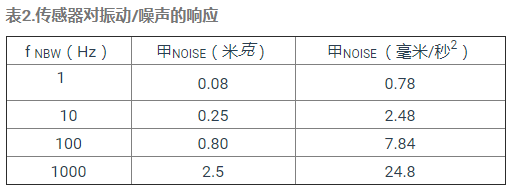
使用公式9中的关系，我们可以估计当在ADXL357上使用具有100 Hz噪声带宽的滤波器（噪声密度=80μg/√Hz）时，总噪声将为0.8 mg（rms）。

速度方面的振动

一些CBM应用需要根据线速度评估核心加速度计行为（范围，带宽，噪声）。进行这种转换的一种方法从图1中的简单模型和产生等式1中的模型的相同假设开始：线性运动，单频率和零平均位移。等式10通过图1中物体的瞬时速度（v V）的数学关系表示该模型。该速度的大小，以均方根（rms）表示，等于峰值速度，除以平方根2。

公式10

公式11采用这种关系的导数产生图1中对象瞬时加速度的关系：

公式11

从等式11的加速度模型的峰值开始，等式12得出一个新的公式，该公式将加速度幅度（A rms）与速度幅度（V rms）和振动频率（f V）联系起来。

公式12

案例分析

让我们将这一切与ADXL357的案例研究结合在一起，ADXL357以线速度表示其振幅频率范围为1 Hz至1000 Hz的范围（峰值ICfans）和分辨率。图5提供了几个属性的图形定义，这些属性将有助于本案例研究，首先是ADXL357在1 Hz至1000 Hz频率范围内的噪声密度图。为了简单在本讨论的目的，所有在此特定情况下研究的计算的将假设噪声密度恒定（φ ND  在整个频率范围= 80微克/√Hz的）。图5中的红色光谱图表示带通滤波器的光谱响应，绿色垂直线表示单个频率的光谱响应（f V）振动，这对于开发基于速度的分辨率和范围估计是有用的。

图5.案例研究噪声密度和过滤。

在此过程中的第一步骤使用等式9来估计噪声（A NOISE即来自四个不同的噪声带宽（F）NBW）：1赫兹，10赫兹，100赫兹和1000赫兹。表2以线性加速度的两种不同测量单位表示这些结果：g和mm / s2。在大多数MEMS加速度计规格表中使用g是相当普遍的，而在这些术语中通常不提供振动度量。幸运的是，g  和mm / s2 之间的关系  是众所周知的，可以在公式13中找到。

公式13

本案例研究的下一步重新排列公式12中的关系，得出一个简单的公式（见公式14），用于将总噪声估计值（从表2中）转换为线速度（V RES，V PEAK）。除了提供这种关系的一般形式之外，公式14还提供了一个具体示例，使用10 Hz的噪声带宽（以及表2中的2.48 mm / s 2的加速度噪声）。图6中的四条虚线表示相对于振动频率（f V）的所有四个噪声带宽的速度分辨率。

公式14

图6.峰值和分辨率与振动频率的关系。

除了显示每个带宽的分辨率外，图6还提供了一条实线蓝线，表示相对于频率的峰值振动水平（线速度）。这来自公式15中的关系，它以与公式14相同的一般形式开始，但不是使用分子中的噪声，而是使用ADXL357可以支持的最大加速度。请注意，假设采用单频振动模型，分子中的√2因子会对此最大加速度进行调整以反映均方根水平。

公式15

最后，红色框表示如何将此信息应用于系统级要求。该红色框的最小（0.28 mm / s）和最大（45 mm / s）速度级别来自机械振动的通用行业标准中的一些分类级别：ISO-10816-1。覆盖ADXL357的范围和分辨率图的要求提供了一种快速的方法来进行简单的观察，例如：

• 测量范围的最坏情况是在最高频率，其中ADXL357的±40 g范围似乎能够测量与ISO-10816-1相关的很大一部分振动曲线。

• 使用噪声带宽为10 Hz滤波器的滤波器处理ADXL357的输出信号时，ADXL357能够在1.5 Hz至1000的频率范围内解析ISO-10816-1（0.28 mm / s）的最低振动水平赫兹。 

• 使用噪声带宽为1 Hz滤波器的滤波器处理ADXL357的输出信号时，ADXL357能够在整个1 Hz至1000 Hz的频率范围内解析ISO-10816-1的最低振动水平。 

结论

MEMS加速度计作为振动传感器已经成熟，它们在现代工厂的CBM系统中看似完美的技术融合风暴中起着关键作用。传感，连接，存储，分析和安全方面的新解决方案汇集在一起，为工厂管理人员提供完全集成的振动观测和过程反馈控制系统。