EEPW论坛

1.概述：

在PCSSVGAPFUPS等电力电子设备，都有设计合适的 滤波器 抑制开关谐波，滤波器在特定的工况下会产生谐振尖峰。比如并网 逆变器 的LCL滤波器受电网 阻抗 影响，PCS离网运行受负载阻抗影响，充电桩多模块并联等由电抗或阻抗变化造成谐振频率变化，就容易产生谐振问题了。

2.LC滤波器谐振原理：

LC滤波器一般应用是典型的二阶电路，串联谐振时电路呈阻性，阻抗最小，电流达到最大也被称为电流谐振，输出是电容上的电压。

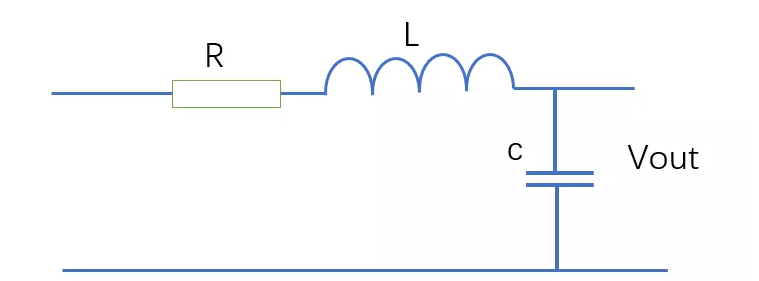
根据KVL建立动态方程：

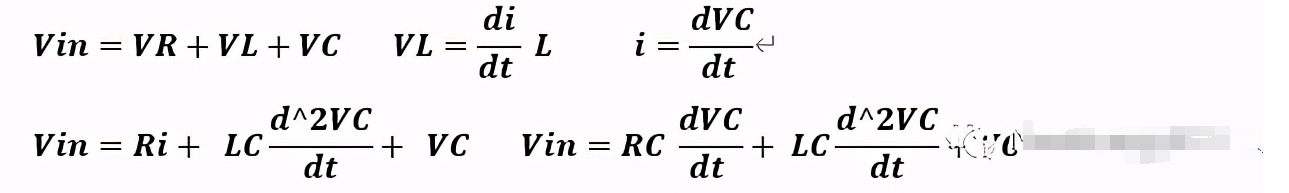
动态方程得到了二阶非齐次方程，如果要解决谐振问题，那么需要找到二阶非齐次方程的通解和特解。二阶非齐次方程比较难求解，把它变成二阶线性微分方程的标准形式和特征方程。

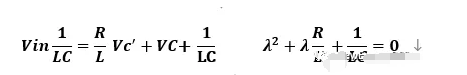
电路微分方程的特征根称为电路的固有频率，RLC取值不同，特征根有三种情况。两个不相等的实数根，过阻尼状态，两个相等实数根，临界阻尼状态。共轭复数根，欠阻尼状态。

过欠阻尼数学模型和函数图像：

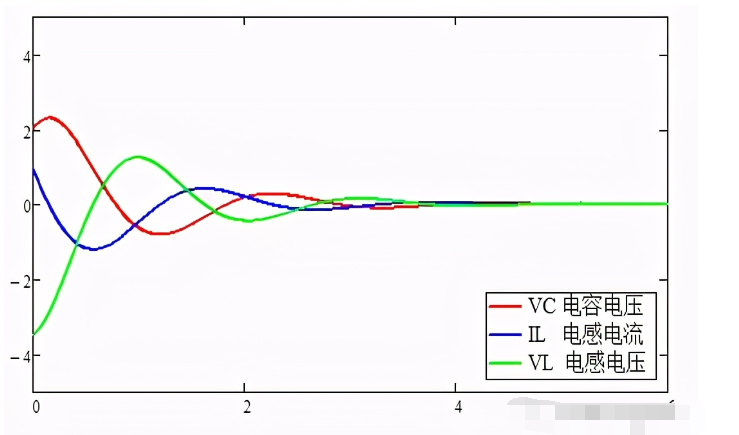
此时衰减震荡，衰减系数和阻尼电阻的取值有关，决定了衰减得快慢。如果阻尼电阻为零，衰减系数为零，就会等幅震荡。电感的磁场和电容的电场，相互交换。

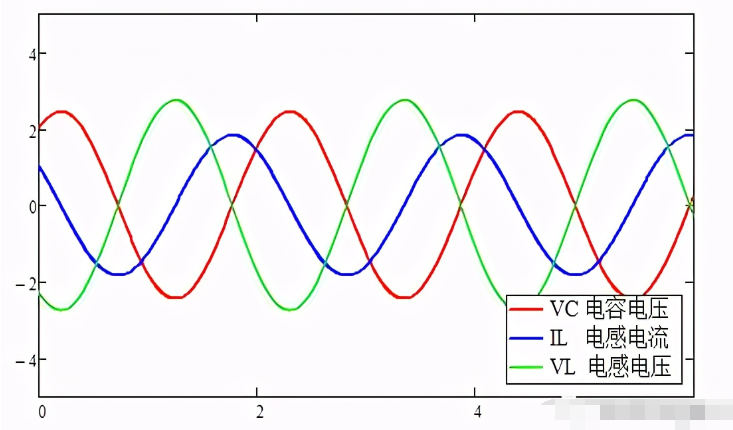
过阻尼函数图像：

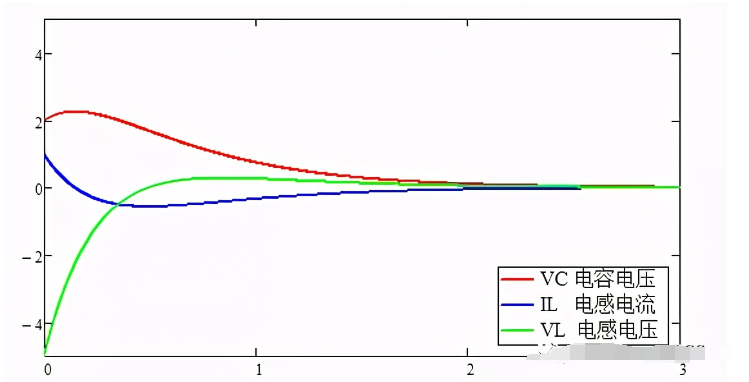
过阻尼放电，临界阻尼类似于指数规律衰减。由于通解公式不同。模型中没有建立。

通过建立时域模型小结：

1.调整阻尼电阻R，R值越大可以发现函数波形越不容震荡，R值越小容易进入欠阻尼。就越容易震荡产生尖峰。

2.调整滤波电容C，C值增大可以发现函数波形幅值变小，C值减小可以发现函数波形幅值变大。

3.调整滤波电感L，，L值减小可以发现函数波形幅值变小，L值增大可以发现函数波形幅值变大。

3.LC滤波器频域分析：

上述用动态方程分析LC滤波器有很多不方便的地方。LC为二阶滤波器，求解微分方程还行，LCL这种三阶微分方程求解就比较复杂了。用传递函数和伯德图来看消除谐振尖峰效果。

传递函数：

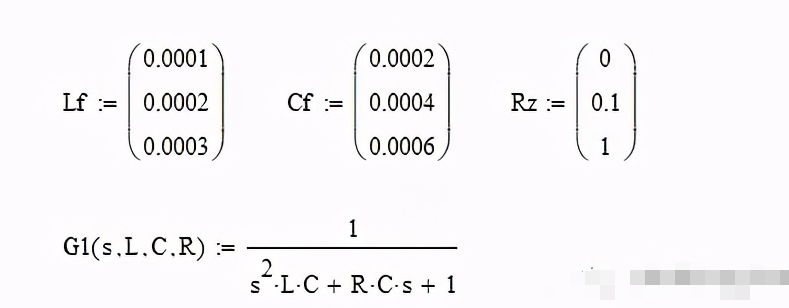
伯德图：

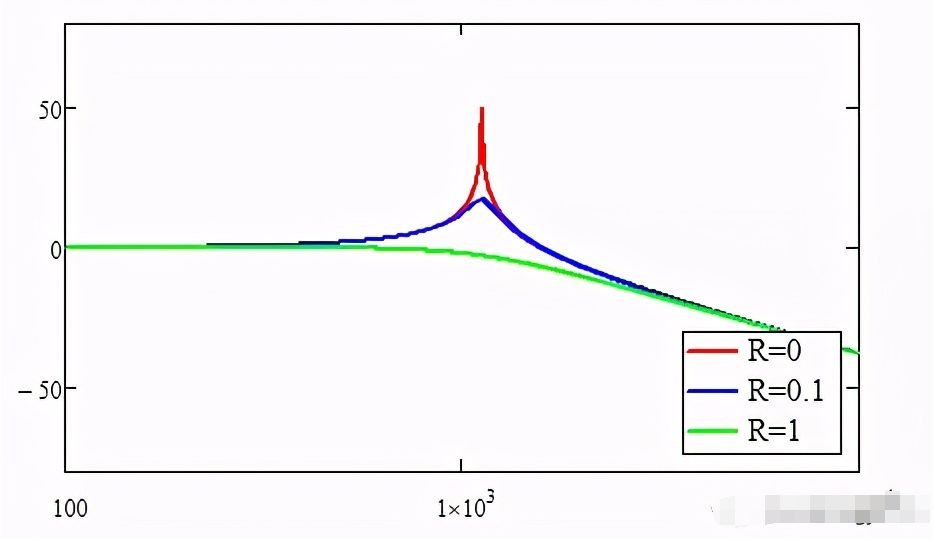
伯德图可以看出不同阻尼电阻的谐振尖峰抑制效果

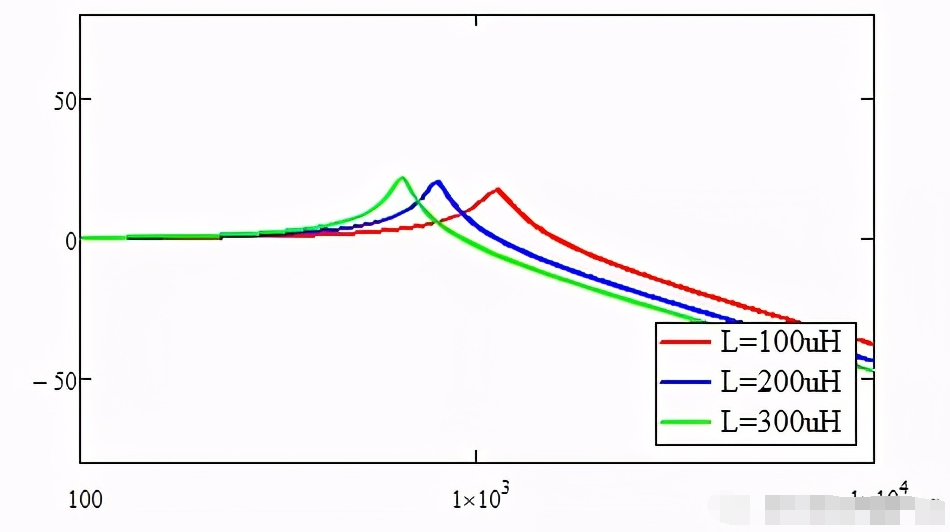
伯德图可以看出不同滤波电感的谐振尖峰抑制效果

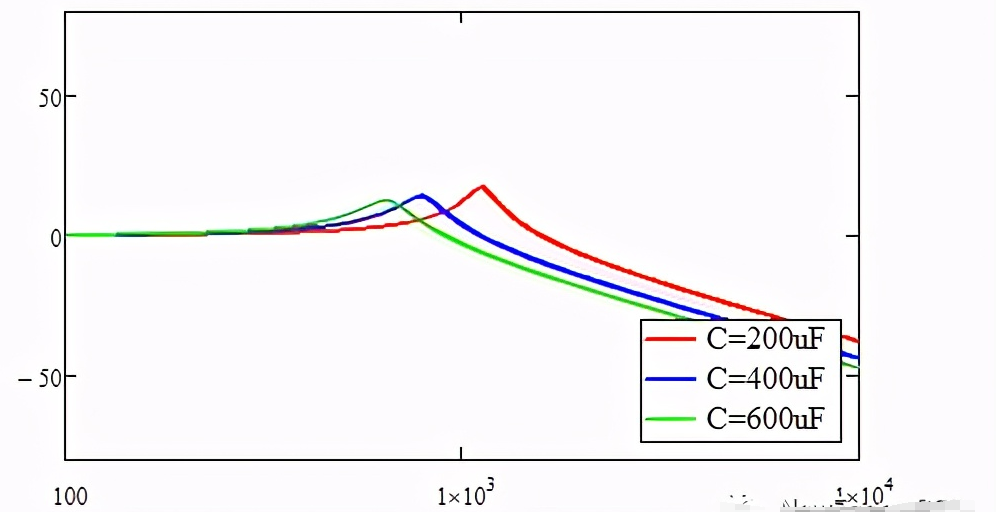
伯德图可以看出不同滤波电容的谐振尖峰抑制效果