EEPW论坛

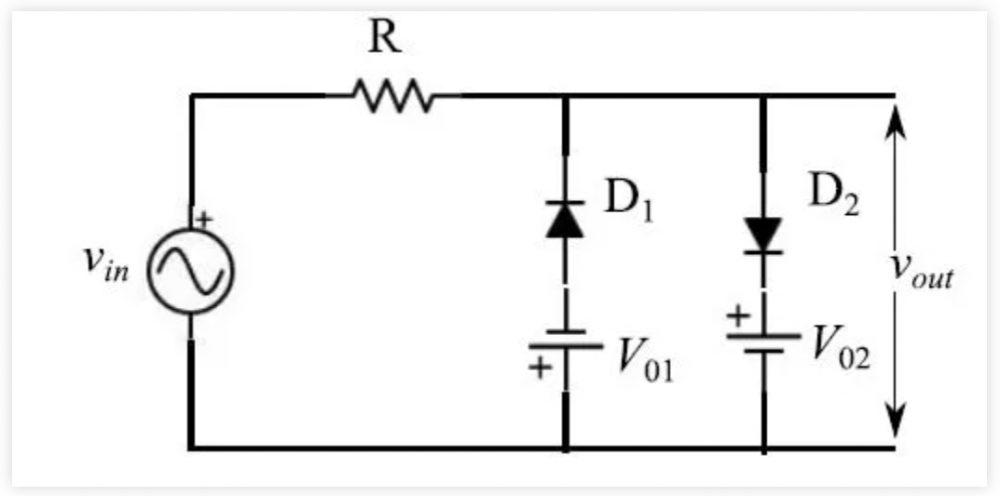
图1. 第一个电池极性反转的双电平限幅器电路

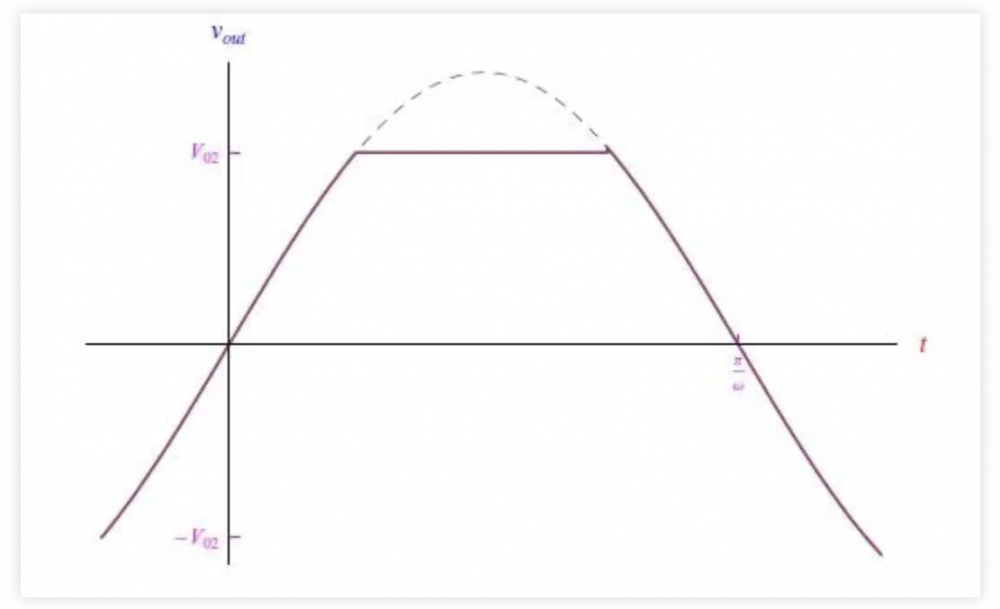
图2. 输出信号趋势通过使用两个串联但方向相反的稳压二极管（齐纳二极管）也可以获得类似的结果。事实上，与正波前相对应，两个二极管中的一个处于反向偏置状态，因此决定了串联中电流的走向。当波前符号反转时，二极管的角色互换，但结果是相同的，因为这两个二极管无论如何都有一个是反向偏置的。如果两个二极管完全相同，则串联电压将从−V_z变为+V_z，即V_z>0，这是单个二极管的齐纳电压。输出的交替周期与输入信号的周期相同。因此，输出为方波。这种简单的分析主要基于两个二极管处于理想条件。在真实条件下，需要稳压二极管的电压-电流特性的解析表达式。为此，我们注意到，与传统二极管相比，稳压二极管的行为更不典型：除了必须在反向偏置下工作之外，其两端的电压必须达到击穿值（V_z）的量级，其行为差不多是渐近的（图3）。在这种工作条件下，即使电流剧烈变化，电压也能保持稳定。然而，为了实现这样的稳压器，稳压二极管的配置必须恰当，因为所有电流变化都是由相应的电压变化引起的，正如上一期文章中已经研究过的情况一样。图3. 稳压二极管的电压-电流特性电压-电流特性可以通过分段函数来仿真，只要各个曲线在对应于-V_z的点处连接即可。连接条件通过施加函数和一阶导数的连续性来表达。第一个条件至关重要，只有这样电流才不会在连接点处发生突变。但第二个条件也很重要，否则，二极管的微分电阻会在连接点处发生突变，而这是不可接受的。经过繁琐而费力的数学分析，我们已经证明不可能同时应用这两个条件，为此我们只选择渐近分支（对于v=−V_z），然后将其扩展到v=0。正是由于这种近似，这里我们有一个非零电流值，正如我们从图3中的图表中看到的。但这并不影响我们的工作，因为工作点无论如何都位于v=−V_z的右邻域内（回想一下我们书写符号的惯例：大写字母表示与时间无关的量，反之亦然，但电流除外，电流我们普遍采用小写字母）。电压-电流特性的解析表达式如下：我们使用的测试电路如图4所示，其中电阻R的值以及V₀都是自由参数。

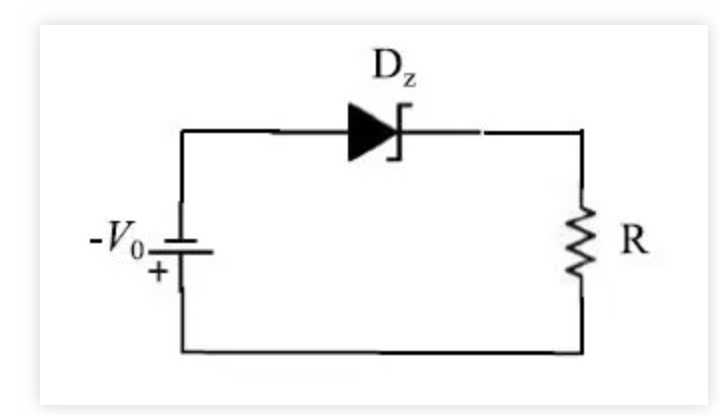
图4. 与给定电阻R串联的稳压二极管我们报告了稳压二极管模型的最终结果，其中Mathematica软件由于反向饱和电流i₀值较小而出现了数值不稳定。因此，我们对二极管两端的电流和压降进行了无量纲化和归一化处理。通过无量纲变量的电流：除此以外，电路会简单地解决：在情况（2）中，无量纲电压-电流特性由下式给出：其中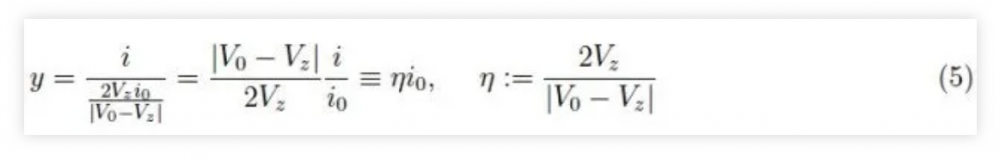：是归一化为ηi₀的电流。通过应用基尔霍夫第二定律，我们有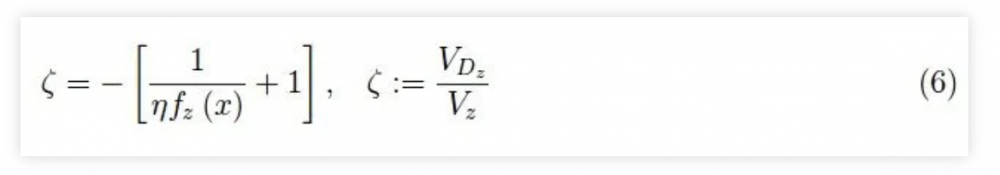：也就是说，稳压二极管两端的压降归一化为V_z。通过研究ζ的符号可以看出，我们的模型在0≤x≤x_max范围内工作，其中最大值让我们能够计算出在V₀=50V、V_z=60V、i₀=1µA时获得的最大电阻，约为50MΩ。