EEPW论坛

以各模块计算具体的传递函数之前，在导出传递函数时，确认两个重要的定律。

一个是指基尔霍夫的电流定律。本定律是指“任意的节点中电流的和为0”。本定律必须要注意的是电流的流向。

另一个是指基尔霍夫的电压定律。本定律是指“任意的闭合电路中电压波动为0”。这两个定律如图3所示。

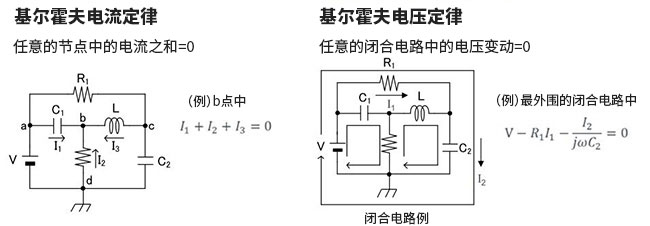
图3

为了导出传递函数而使用上面两个定律，但是有一件事必须要探讨。那就是如何表述阻抗。如下面的图4所示，电阻R、电容C、线圈L连接于DC电源V，各自的变动不同。电阻R两端的电压不随时间的推移变化。电容器的电压逐步上升，一定时间后达到电源的电压。 线圈的电压立刻达到电源的电压，逐步下降。

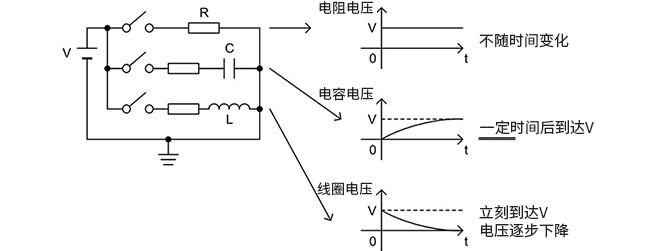
图4

从图4的特性可以认为，以电容器和线圈以及电阻考虑时，电阻值（阻抗）可以作为时间（相位）的函数。这样，包括随时间变化的电阻，都可以表述为阻抗。可以说输入电压为步进响应时的电容器的阻抗随时间的推移变大。线圈与其相反。电路的场合，因为作为时间的倒数而使用角速度ω、可以表示为如图5所示。

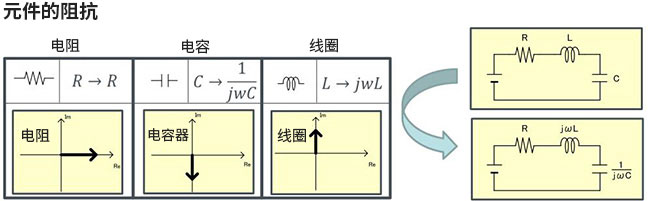
图5

最后，解释出现复数的原因。电路中复数表示相位，是响应时间相关的参数。这种情况，表示电源的响应速度。电容器的情况为延迟后到达电源电压V，线圈与其相反，可以表示为如图5所示。