| 我们提出了一种处理傅里叶变换的方法,其并不需要二次多项式相位项的抽样,而是用解析的方法处理。我们提出该理论的同时也给出了几个例子证明其潜力。 1.简介 物理光学建模需要频繁地从空间转换到角频域,反之亦然。这可以由电场和磁场分量的傅里叶变换得到。所以,快速傅里叶变换(FFT)算法成了快速物理光学建模的支柱[1]。FFT技术的数值计算量与场分量复振幅所需采样点的数量近似成线性关系。在光学中,我们经常处理有强波阵面相位的场分量,例如:球形。但是由于2π模,平滑的波阵面相位的复抽样导致了大量的数值计算工作,甚至在FFT中也是如此。 2.理论2.1 场的表征:提取二次相位 我们从空间域的符号开始,在本文中我们使用符号 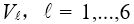 对应6个场分量,也就是V = (E, H): 对应6个场分量,也就是V = (E, H):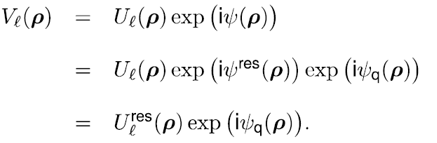 (1) (1)在公式1中,我们假设场 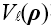 有两部分:衍射场 有两部分:衍射场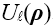 和一个平滑的波阵面相位exp(iψ(ρ))。对于得到的结果,我们从波阵面相位中提取二次相位exp(iψ(ρ))并且将余下的部分认为是余项场 和一个平滑的波阵面相位exp(iψ(ρ))。对于得到的结果,我们从波阵面相位中提取二次相位exp(iψ(ρ))并且将余下的部分认为是余项场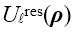 。假设exp(iψ(ρ))可由其实数系数C和D = (Dx, Dy)给出: 。假设exp(iψ(ρ))可由其实数系数C和D = (Dx, Dy)给出: 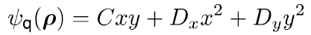 (2)显然,在强二次相位情况中,全场 (2)显然,在强二次相位情况中,全场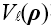 比余项场需要更多的抽样量。所以,我们的目标是通过FFT且无二次相位项exp(iψ(ρ))抽样的情况下,计算V(ρ)的傅里叶变换。 比余项场需要更多的抽样量。所以,我们的目标是通过FFT且无二次相位项exp(iψ(ρ))抽样的情况下,计算V(ρ)的傅里叶变换。2.2.半解析傅里叶变换 从卷积定理可知: 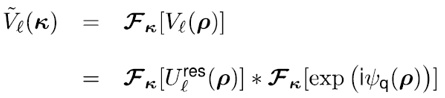 (3) (3)通常来说,项 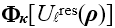 必须进行数值计算处理。另一方面,从数学角度[2]我们可知: 必须进行数值计算处理。另一方面,从数学角度[2]我们可知: 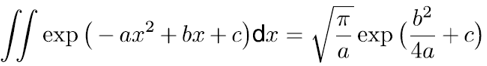 (4) (4)适用于任何复 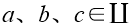 ,只要R{a} ≥ 0且a ≠ 0。在该数学工具的帮助下,项κ[exp(iψ(ρ))]的解析表征可以推导出来: ,只要R{a} ≥ 0且a ≠ 0。在该数学工具的帮助下,项κ[exp(iψ(ρ))]的解析表征可以推导出来: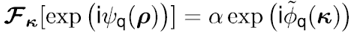 (5)其中: (5)其中: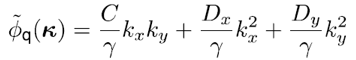 (6)其中常数项 (6)其中常数项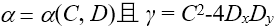 。将公式5带入公式3,通过改变卷积和傅里叶变换积分的阶次,我们发现 。将公式5带入公式3,通过改变卷积和傅里叶变换积分的阶次,我们发现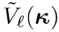 可以表示为: 可以表示为: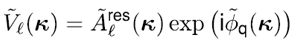 (7)其中: (7)其中: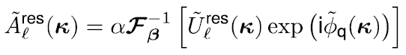 (8)这里, (8)这里, 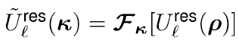 和坐标项 和坐标项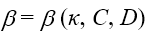 。公式7-8是半解析傅里叶变换的数学表达式。它表示全场的FFT可被两个余项场的FFT替代。 。公式7-8是半解析傅里叶变换的数学表达式。它表示全场的FFT可被两个余项场的FFT替代。3.数值仿真 这些概念在物理光学建模和设计软件Wyrowski VirtualLab Fusion[3]中实现。 3.1.有效性测试1:纯二次相位 在第一组测试中,我们准备了余项场 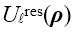 ,其幅度信息如图1所示,且相位为零。我们将不同的二次相位项exp(iψq(ρ))与之相乘,组成 ,其幅度信息如图1所示,且相位为零。我们将不同的二次相位项exp(iψq(ρ))与之相乘,组成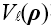 。然后我们分别对全场 。然后我们分别对全场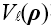 应用FFT和半解析FFT。 应用FFT和半解析FFT。  图2展示了不同情况下FFT和半解析FFT所需的采样点。可以发现当场有强二次相位时,半解析FFT需要比FFT少得多的抽样点。 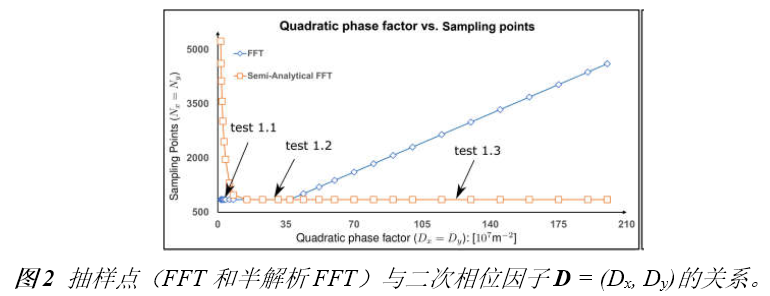 在图3中我们给出了三个典型位置的角频谱的振幅。解释了波阵面相位的物理意义,因此当波阵面相位非常小时,在FT中衍射效应占主导地位。否则,当波阵面相位增加时,FT展现了越来越多的几何特征。  3.2 有效性测试2:球形相位在第二组中,我们将乘上另一种相位:球形相位 3.2 有效性测试2:球形相位在第二组中,我们将乘上另一种相位:球形相位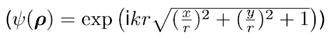 。不像测试1,我们只能用解析方法处理二次部分而不能处理整个球形相位。所以,余项场的相位不再是零而是球形和二次相位之间的差值,并且它会随着球半径r的减小而越来越大。不同情况下FFT和半解析FFT的抽样点于图4给出。结果显示在强球形相位情况下,由于相位差, 。不像测试1,我们只能用解析方法处理二次部分而不能处理整个球形相位。所以,余项场的相位不再是零而是球形和二次相位之间的差值,并且它会随着球半径r的减小而越来越大。不同情况下FFT和半解析FFT的抽样点于图4给出。结果显示在强球形相位情况下,由于相位差,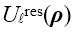 需要更多的抽样点,这导致了半解析FT的抽样数量同样增加了。 需要更多的抽样点,这导致了半解析FT的抽样数量同样增加了。 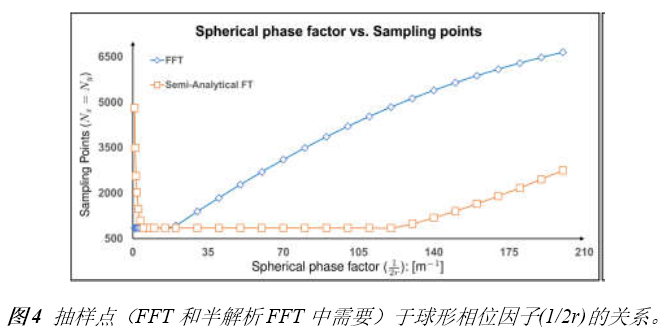 4.结论我们论证了半解析FFT的推导并且展示了几个数值例子。事实表明,半解析FFT的采样仅取决于余项场。在波阵面相位较强的场中,半解析FFT需要的采样点明显较少。 |
共3条
1/1 1 跳转至页
半解析快速傅里叶变换
共3条
1/1 1 跳转至页
回复
| 有奖活动 | |
|---|---|
| 硬核工程师专属补给计划——填盲盒 | |
| “我踩过的那些坑”主题活动——第002期 | |
| 【EEPW电子工程师创研计划】技术变现通道已开启~ | |
| 发原创文章 【每月瓜分千元赏金 凭实力攒钱买好礼~】 | |
| 【EEPW在线】E起听工程师的声音! | |
| 高校联络员开始招募啦!有惊喜!! | |
| 【工程师专属福利】每天30秒,积分轻松拿!EEPW宠粉打卡计划启动! | |
| 送您一块开发板,2025年“我要开发板活动”又开始了! | |
 我要赚赏金打赏帖 我要赚赏金打赏帖 |
|
|---|---|
| 在FireBeetle2ESP32-C5上实现温湿度检测和显示被打赏¥20元 | |
| 在FireBeetle2ESP32-C5上实现光照强度检测及显示被打赏¥21元 | |
| 以FireBeetle2ESP32-C5实现数据识读播报被打赏¥19元 | |
| 【STM32F103ZET6】14:实测STM32F1的串口输出任务的挂起与恢复功能被打赏¥27元 | |
| Chaos-nano在压力容器监控系统中的项目应用被打赏¥23元 | |
| 基于FireBeetle2ESP32-C5的WS2812B彩色灯带控制被打赏¥21元 | |
| SWM221CBT7显示开发板驱动TFT显示屏被打赏¥19元 | |
| SWM221CBT7显示开发板驱动OLED屏显示被打赏¥19元 | |
| SWM221CBT7显示开发板及其使用被打赏¥20元 | |
| 揭秘Chaos-nano:ArduinoProMini轻量级操作系统开发框架深度解析与实战应用被打赏¥19元 | |



