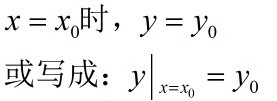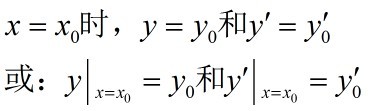|
含有未知函数的导数的方程,称之为微分方程。 微分方程中所出现的未知函数的最高阶导数的阶数,叫做微分方程的阶。下面是一个四阶微分方程的例子:
一般的,解决实际问题时,首先建立微分方程(比如前一篇BLOG建立的一阶电路微分方程),然后找到满足微分方程的函数。这个函数就叫做该微分方程的解。
如果微分方程的解中含有任意常数,且任意常数的个数与微分方程的阶数相同,这样的解叫做微分方程的通解。函数
为了完全反映客观事物的规律,必须求出通解中的常数项。因此需要给定一些条件。对于一阶未知函数
如果微分方程是二阶的,则所需要的条件是:
确定了通解中的任意常数后,就得到了微分方程的特解。 |
共5条
1/1 1 跳转至页
微分方程-1
共5条
1/1 1 跳转至页
 含有
含有 ,通常用来确定任意常数的条件是:(其中x0,y0都是给定的值)
,通常用来确定任意常数的条件是:(其中x0,y0都是给定的值)